Question

$\int_{0}^{\pi/4}sec^4x \,dx$

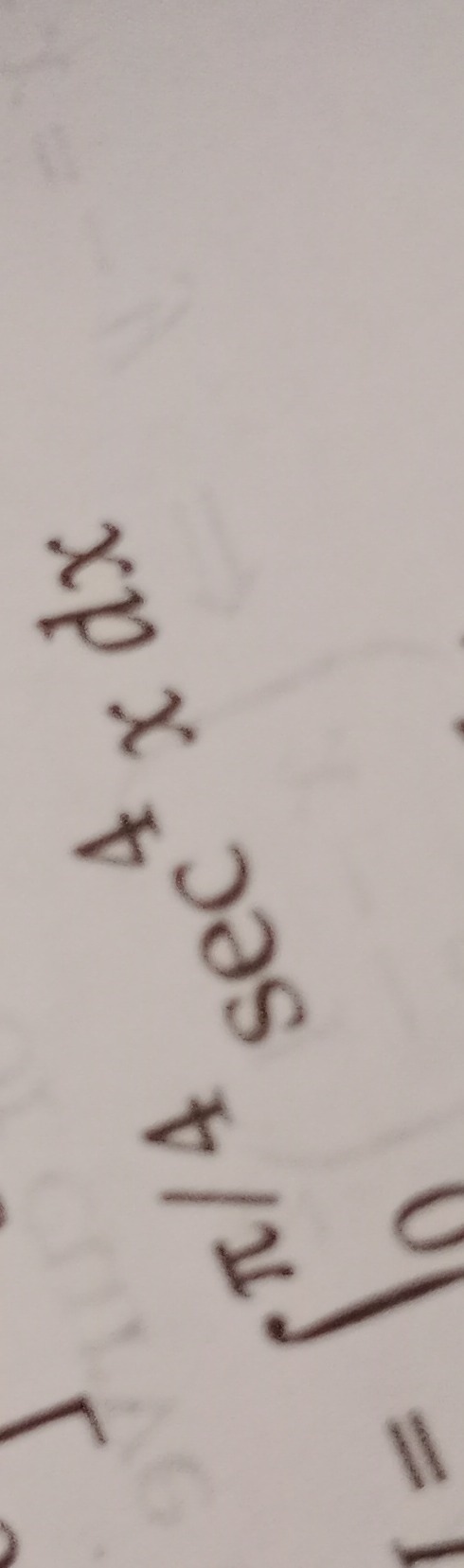
Answer 1

$\frac{4}{3}$

Answer 2

Let

$u = \tan x \quad \Rightarrow \quad du = \sec^2 x\,dx$.

Since

$\sec^4 x\,dx = \sec^2 x (\sec^2 x\,dx) = \sec^2 x\,du$,

and noting that $\sec^2x = 1+\tan^2x = 1+u^2$, the integral becomes

$\int_{x=0}^{\pi/4}\sec^4 x\,dx = \int_{u=0}^{1}(1+u^2)\,du$.

Integrate:

$\int_0^1 (1+u^2)\,du = \left[u + \frac{u^3}{3}\right]_0^1 = 1 + \frac{1}{3} = \frac{4}{3}$.