Question

$\int_{0}^{\pi/2}sin^{-1}x dx$

Answer 1

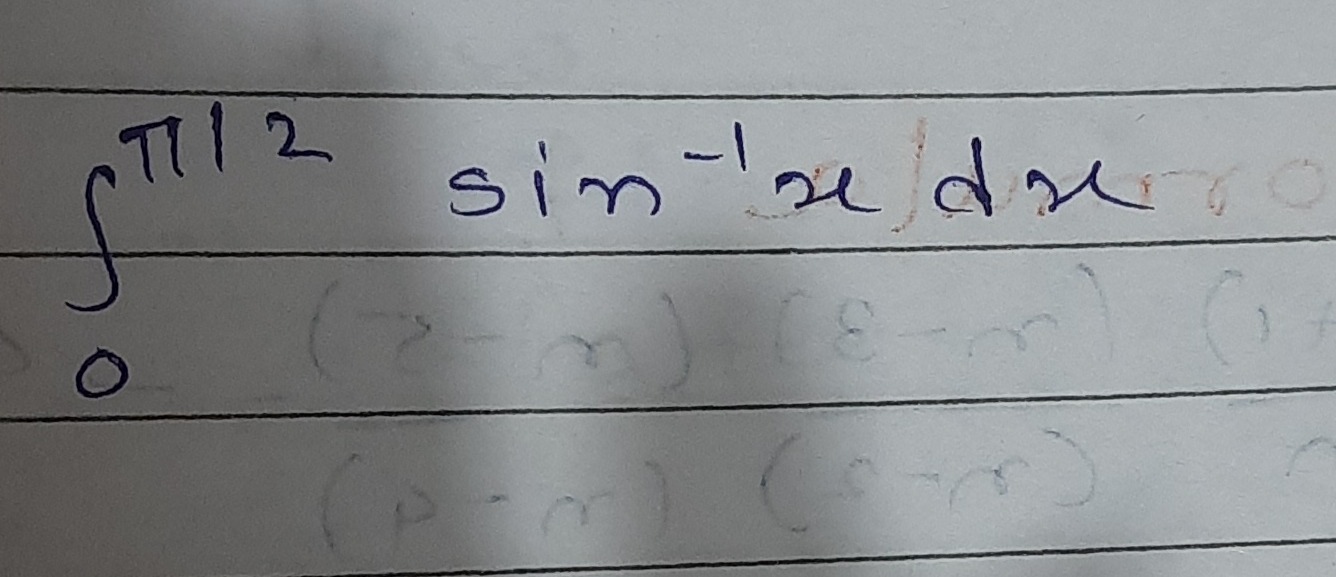
The integral is undefined in the real number system. Assuming the intended integral was $\int_{0}^{1} \sin^{-1}x \, dx$, the answer is $\frac{\pi}{2} - 1$.

Answer 2

The given integral is $\int_{0}^{\pi/2} \sin^{-1}x \, dx$.

1. Domain Check:

The domain of the function $\sin^{-1}x$ is $[-1, 1]$. The upper limit of integration is $\pi/2$, which is approximately $1.57$. Since $\pi/2 > 1$, the function $\sin^{-1}x$ is not defined for $x \in (1, \pi/2]$ in the real number system. Therefore, the integral as stated is undefined in real calculus.

2. Assumption of Typo:

It is highly probable that there is a typo in the question and the upper limit of integration was intended to be $1$, making the integral $\int_{0}^{1} \sin^{-1}x \, dx$. We will proceed with solving this modified integral.

3. Solution for $\int_{0}^{1} \sin^{-1}x \, dx$:

We use integration by parts, which states $\int u \, dv = uv - \int v \, du$. Let $u = \sin^{-1}x$ and $dv = dx$. Then, $du = \frac{1}{\sqrt{1-x^2}} dx$ and $v = x$.

Applying the integration by parts formula: $\int_{0}^{1} \sin^{-1}x \, dx = [x \sin^{-1}x]_{0}^{1} - \int_{0}^{1} x \frac{1}{\sqrt{1-x^2}} dx$

Step 1: Evaluate the first term $[x \sin^{-1}x]_{0}^{1} = (1 \cdot \sin^{-1}(1)) - (0 \cdot \sin^{-1}(0))$ $= (1 \cdot \frac{\pi}{2}) - (0 \cdot 0) = \frac{\pi}{2}$

Step 2: Evaluate the second integral Let $I_2 = \int_{0}^{1} \frac{x}{\sqrt{1-x^2}} dx$. To solve this, use substitution. Let $t = 1-x^2$. Then, $dt = -2x \, dx$, which implies $x \, dx = -\frac{1}{2} dt$. Change the limits of integration for $t$: When $x=0$, $t = 1-0^2 = 1$. When $x=1$, $t = 1-1^2 = 0$.

Substitute these into $I_2$: $I_2 = \int_{1}^{0} \frac{1}{\sqrt{t}} \left(-\frac{1}{2}\right) dt$ $I_2 = -\frac{1}{2} \int_{1}^{0} t^{-1/2} dt$ Swap the limits and change the sign of the integral: $I_2 = \frac{1}{2} \int_{0}^{1} t^{-1/2} dt$ Integrate $t^{-1/2}$: $I_2 = \frac{1}{2} \left[ \frac{t^{-1/2+1}}{-1/2+1} \right]_{0}^{1}$ $I_2 = \frac{1}{2} \left[ \frac{t^{1/2}}{1/2} \right]_{0}^{1}$ $I_2 = \frac{1}{2} [2\sqrt{t}]_{0}^{1}$ $I_2 = [\sqrt{t}]_{0}^{1}$ $I_2 = \sqrt{1} - \sqrt{0} = 1 - 0 = 1$

Step 3: Combine the results Substitute the values back into the integration by parts formula: $\int_{0}^{1} \sin^{-1}x \, dx = \frac{\pi}{2} - I_2 = \frac{\pi}{2} - 1$

The final answer is $\frac{\pi}{2} - 1$.

Explanation of the solution:

The original integral $\int_{0}^{\pi/2} \sin^{-1}x \, dx$ is undefined in real numbers because $\sin^{-1}x$ is defined only for $x \in [-1, 1]$, and $\pi/2 > 1$. Assuming a common typo, the integral is evaluated as $\int_{0}^{1} \sin^{-1}x \, dx$. This is solved using integration by parts, $\int u \, dv = uv - \int v \, du$, with $u = \sin^{-1}x$ and $dv = dx$. The first part $[x \sin^{-1}x]_{0}^{1}$ evaluates to $\pi/2$. The second integral $\int_{0}^{1} x \frac{1}{\sqrt{1-x^2}} dx$ is solved using substitution $t = 1-x^2$, yielding a value of $1$. Combining these results gives $\frac{\pi}{2} - 1$.