Question

$\int_{0}^{\pi/2}sin^{-1}x dx$

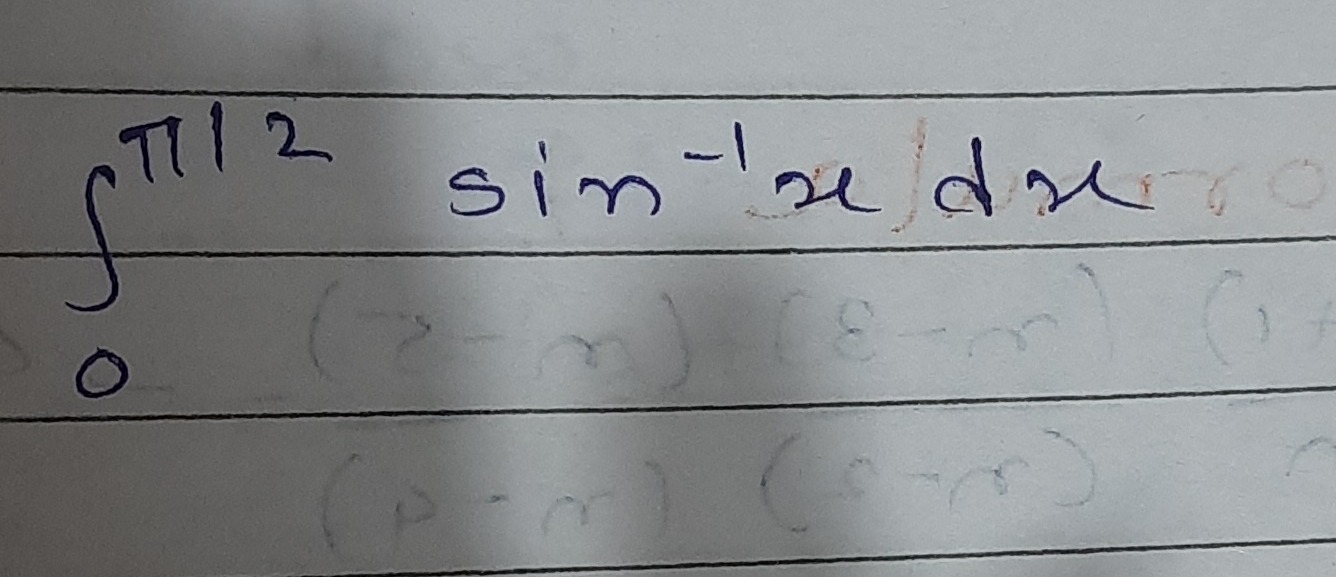
Answer 1

$\frac{\pi}{2} - 1$

Answer 2

The given integral $\int_{0}^{\pi/2}sin^{-1}x dx$ is undefined because $sin^{-1}x$ is not defined for $x > 1$, and $\pi/2 > 1$. Assuming a common typo, the integral is solved for $\int_{0}^{1}sin^{-1}x dx$. This is evaluated using integration by parts: $\int u dv = uv - \int v du$, with $u = sin^{-1}x$ and $dv = dx$. The first term evaluates to $[x sin^{-1}x]_0^1 = \pi/2$. The second integral $\int_0^1 \frac{x}{\sqrt{1-x^2}} dx$ is solved by substitution ($t=1-x^2$), yielding $1$. Subtracting these results gives $\pi/2 - 1$.