Question
Question: Evaluate the definite integral: $\int_{0}^{\pi/2} \sin x \cos 2x \, dx$...
Evaluate the definite integral:
∫0π/2sinxcos2xdx
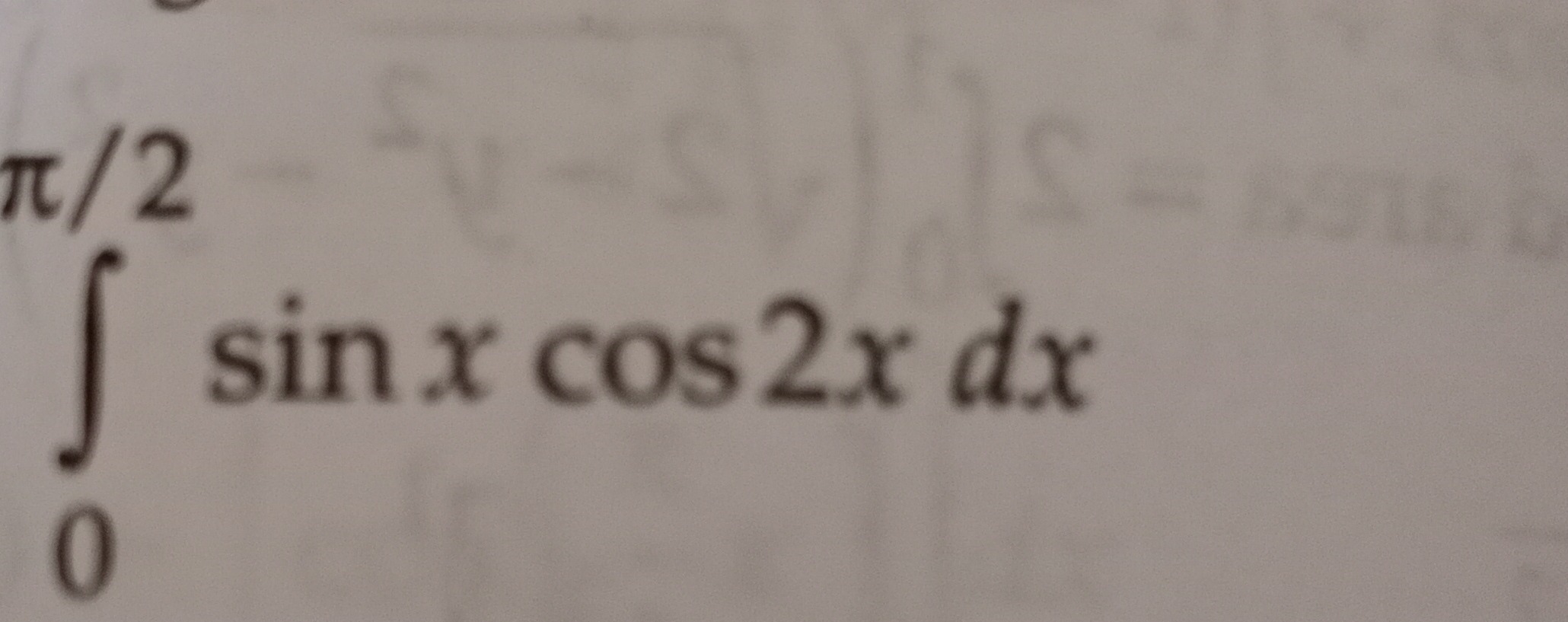
-1/3
1/3
-2/3
2/3
-1/3
Solution
To evaluate the integral ∫0π/2sinxcos2xdx, we can use the product-to-sum trigonometric identity:
sinAcosB=21[sin(A+B)+sin(A−B)]
In our case, A=x and B=2x, so:
sinxcos2x=21[sin(x+2x)+sin(x−2x)]=21[sin(3x)−sin(x)]
Now, we can rewrite the integral as:
∫0π/2sinxcos2xdx=21∫0π/2[sin(3x)−sin(x)]dx
We can split the integral into two parts:
21[∫0π/2sin(3x)dx−∫0π/2sin(x)dx]
Now, we evaluate each integral separately:
-
∫0π/2sin(3x)dx=[−31cos(3x)]0π/2=−31cos(23π)−(−31cos(0))=−31(0)+31(1)=31
-
∫0π/2sin(x)dx=[−cos(x)]0π/2=−cos(2π)−(−cos(0))=−0+1=1
Substitute these results back into the original expression:
21[31−1]=21[−32]=−31
Therefore, the value of the definite integral is −31.
