Question
Question: $\int_{0}^{\pi/2} \frac{\sin x \cos x dx}{\cos^2 x+3 \cos x+2} =$...
∫0π/2cos2x+3cosx+2sinxcosxdx=
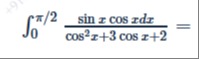
ln(9/8)
Solution
Let the integral be I. I=∫0π/2cos2x+3cosx+2sinxcosxdx Let u=cosx. Then du=−sinxdx. When x=0, u=cos(0)=1. When x=π/2, u=cos(π/2)=0. Substituting these into the integral, we get: I=∫10u2+3u+2u(−du) I=∫10u2+3u+2−udu We can swap the limits of integration by changing the sign of the integral: I=∫01u2+3u+2udu Factor the denominator: u2+3u+2=(u+1)(u+2). So the integral becomes: I=∫01(u+1)(u+2)udu We use partial fraction decomposition for the integrand: (u+1)(u+2)u=u+1A+u+2B Multiplying both sides by (u+1)(u+2), we get: u=A(u+2)+B(u+1) To find A, set u=−1: −1=A(−1+2)+B(−1+1)⟹−1=A(1)+B(0)⟹A=−1 To find B, set u=−2: −2=A(−2+2)+B(−2+1)⟹−2=A(0)+B(−1)⟹−2=−B⟹B=2 So, the integrand is: (u+1)(u+2)u=u+1−1+u+22 Now, we integrate the decomposed fractions: I=∫01(u+22−u+11)du I=[2ln∣u+2∣−ln∣u+1∣]01 Evaluate the definite integral at the limits: I=(2ln∣1+2∣−ln∣1+1∣)−(2ln∣0+2∣−ln∣0+1∣) I=(2ln3−ln2)−(2ln2−ln1) Since ln1=0: I=(2ln3−ln2)−(2ln2−0) I=2ln3−ln2−2ln2 I=2ln3−3ln2 Using the logarithm property alnb=ln(ba): I=ln(32)−ln(23) I=ln9−ln8 Using the logarithm property lna−lnb=ln(a/b): I=ln(89)
