Question
Question: $\int_{0}^{\pi/2} cos^{1/2} x \ dx$...
∫0π/2cos1/2x dx
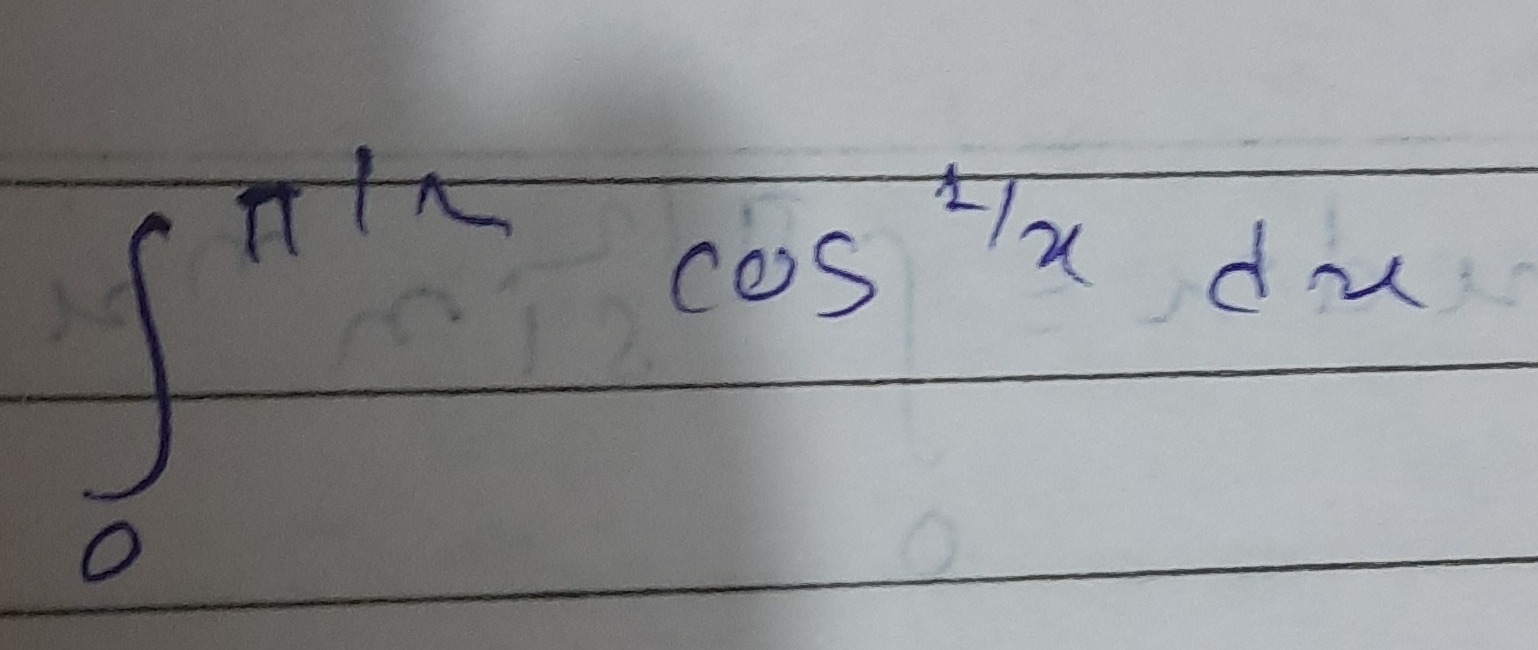
Γ(41)2πΓ(43)
Solution
To evaluate the definite integral ∫0π/2cos1/2x dx, we can use the properties of Beta and Gamma functions.
The integral is of the form ∫0π/2sinmxcosnx dx.
In our case, m=0 and n=1/2.
The general formula for this type of integral in terms of Gamma functions is: ∫0π/2sinmxcosnx dx=2Γ(2m+n+2)Γ(2m+1)Γ(2n+1)
Substitute m=0 and n=1/2 into the formula: ∫0π/2cos1/2x dx=2Γ(20+1/2+2)Γ(20+1)Γ(21/2+1) =2Γ(25/2)Γ(21)Γ(23/2) =2Γ(45)Γ(21)Γ(43)
Now, we use the following properties of the Gamma function:
- Γ(21)=π
- Γ(z+1)=zΓ(z)
Applying the second property to Γ(45): Γ(45)=Γ(1+41)=41Γ(41)
Substitute these values back into the expression: ∫0π/2cos1/2x dx=2(41Γ(41))πΓ(43) =21Γ(41)πΓ(43) =Γ(41)2πΓ(43)
This is the most simplified form of the integral in terms of Gamma functions. The values of Γ(1/4) and Γ(3/4) are not elementary and are usually left in this form in competitive exams unless specific numerical approximations or further properties are required.
