Question
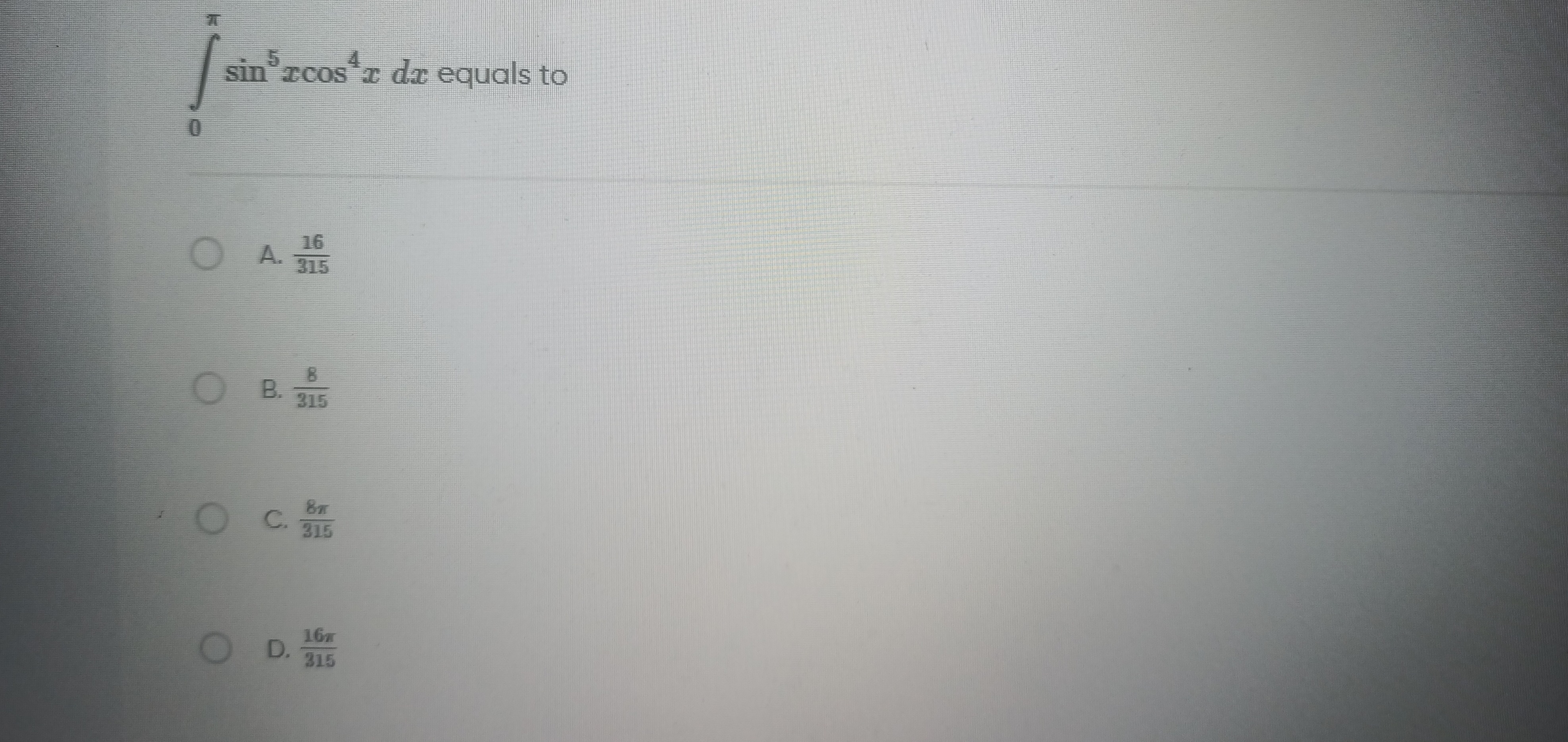
Question: $\int_{0}^{\pi} \sin^{5}x \cos^{4}x \,dx$ equals to...
∫0πsin5xcos4xdx equals to
A
31516
B
3158
C
3158π
D
31516π
Answer
31516
Explanation
Solution
Let I=∫0πsin5xcos4xdx. We use the property ∫0af(x)dx=∫0af(a−x)dx. Let f(x)=sin5xcos4x. Then f(π−x)=sin5(π−x)cos4(π−x)=(sinx)5(−cosx)4=sin5xcos4x=f(x). Thus, I=∫0πsin5xcos4xdx=2∫0π/2sin5xcos4xdx. Let u=cosx, then du=−sinxdx. When x=0, u=1. When x=π/2, u=0. sin5xcos4x=sin4xcos4xsinx=(1−cos2x)2cos4xsinx=(1−u2)2u4(−du). So, I=2∫10(1−u2)2u4(−du)=2∫01(1−2u2+u4)u4du I=2∫01(u4−2u6+u8)du=2[5u5−72u7+9u9]01 I=2(51−72+91)=2(31563−90+35)=2(3158)=31516.
