Question
Question: $\int_{0}^{\pi} \frac{x \cos x}{(1 + \sin x)^2} dx$...
∫0π(1+sinx)2xcosxdx
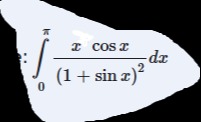
2 - \pi
Solution
To evaluate the integral I=∫0π(1+sinx)2xcosxdx, we use integration by parts. The formula for integration by parts is ∫udv=uv−∫vdu.
Let u=x and dv=(1+sinx)2cosxdx.
First, find du and v: du=dx.
To find v, integrate dv: v=∫(1+sinx)2cosxdx. Let t=1+sinx. Then dt=cosxdx. So, v=∫t2dt=−t1=−1+sinx1.
Now, substitute these into the integration by parts formula: I=[x(−1+sinx1)]0π−∫0π(−1+sinx1)dx I=[−1+sinxx]0π+∫0π1+sinx1dx
Evaluate the first term: [−1+sinxx]0π=(−1+sinππ)−(−1+sin00) Since sinπ=0 and sin0=0: =(−1+0π)−(−1+00) =−π−0=−π.
Now, we need to evaluate the second integral: J=∫0π1+sinx1dx. We can simplify the integrand by multiplying the numerator and denominator by (1−sinx): J=∫0π(1+sinx)(1−sinx)1−sinxdx=∫0π1−sin2x1−sinxdx J=∫0πcos2x1−sinxdx=∫0π(cos2x1−cos2xsinx)dx J=∫0π(sec2x−secxtanx)dx
The antiderivative of sec2x−secxtanx is tanx−secx. However, tanx and secx are undefined at x=π/2, which is within the integration interval [0,π]. Thus, we must evaluate the integral as an improper integral or use a property of definite integrals.
Using the property ∫02af(x)dx=2∫0af(x)dx if f(2a−x)=f(x). Let f(x)=1+sinx1. Here 2a=π, so a=π/2. f(π−x)=1+sin(π−x)1=1+sinx1=f(x). So, J=∫0π1+sinx1dx=2∫0π/21+sinx1dx.
Now, we evaluate J′=∫0π/2(sec2x−secxtanx)dx. J′=[tanx−secx]0π/2. Since the antiderivative is undefined at π/2, we take the limit: J′=limb→π/2−(tanb−secb)−(tan0−sec0) J′=limb→π/2−(cosbsinb−cosb1)−(0−1) J′=limb→π/2−(cosbsinb−1)+1. This limit is of the form 0/0, so we apply L'Hopital's rule: J′=limb→π/2−(−sinbcosb)+1 J′=−sin(π/2)cos(π/2)+1=−10+1=0+1=1.
So, ∫0π/21+sinx1dx=1. Therefore, J=2×1=2.
Substitute this value back into the expression for I: I=−π+J I=−π+2.
The final answer is 2−π.
