Question

$\int_{0}^{\pi} (a^{2}cos^{2}x + b^{2}sin^{2}x)^{2} dx$

Answer 1

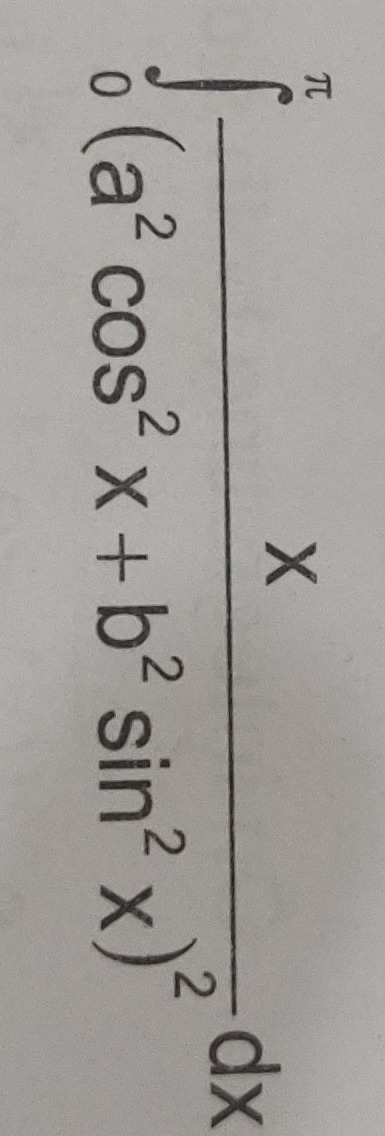
$\frac{\pi}{8}(3a^{4} + 3b^{4} + 2a^{2}b^{2})$

Answer 2

To evaluate the definite integral $I = \int_{0}^{\pi} (a^{2}cos^{2}x + b^{2}sin^{2}x)^{2} dx$, we will follow these steps:

1. Expand the integrand.
2. Use trigonometric identities to reduce the powers of $\cos x$ and $\sin x$.
3. Integrate each term over the interval $[0, \pi]$.
4. Sum the results.

Step 1: Expand the integrand

The integrand is $(a^{2}cos^{2}x + b^{2}sin^{2}x)^{2}$. Expanding this gives:

$(a^{2}cos^{2}x + b^{2}sin^{2}x)^{2} = (a^{2}cos^{2}x)^{2} + (b^{2}sin^{2}x)^{2} + 2(a^{2}cos^{2}x)(b^{2}sin^{2}x)$ $= a^{4}cos^{4}x + b^{4}sin^{4}x + 2a^{2}b^{2}cos^{2}x sin^{2}x$

So, the integral becomes:

$I = \int_{0}^{\pi} (a^{4}cos^{4}x + b^{4}sin^{4}x + 2a^{2}b^{2}cos^{2}x sin^{2}x) dx$ $I = a^{4}\int_{0}^{\pi} cos^{4}x dx + b^{4}\int_{0}^{\pi} sin^{4}x dx + 2a^{2}b^{2}\int_{0}^{\pi} cos^{2}x sin^{2}x dx$

Step 2: Evaluate each integral separately using trigonometric identities

We use the following identities:

$cos^{2}x = \frac{1+cos(2x)}{2}$ $sin^{2}x = \frac{1-cos(2x)}{2}$ $cos^{2}(2x) = \frac{1+cos(4x)}{2}$ $sin^{2}(2x) = \frac{1-cos(4x)}{2}$ $sin x cos x = \frac{sin(2x)}{2}$

Integral 1: $\int_{0}^{\pi} cos^{4}x dx$

$cos^{4}x = (cos^{2}x)^{2} = \left(\frac{1+cos(2x)}{2}\right)^{2} = \frac{1+2cos(2x)+cos^{2}(2x)}{4}$

Substitute $cos^{2}(2x) = \frac{1+cos(4x)}{2}$:

$cos^{4}x = \frac{1+2cos(2x)+\frac{1+cos(4x)}{2}}{4} = \frac{2+4cos(2x)+1+cos(4x)}{8} = \frac{3+4cos(2x)+cos(4x)}{8}$

Now, integrate:

$\int_{0}^{\pi} cos^{4}x dx = \int_{0}^{\pi} \frac{3+4cos(2x)+cos(4x)}{8} dx$ $= \frac{1}{8} \left[3x + \frac{4sin(2x)}{2} + \frac{sin(4x)}{4}\right]_{0}^{\pi}$ $= \frac{1}{8} \left[3x + 2sin(2x) + \frac{sin(4x)}{4}\right]_{0}^{\pi}$ $= \frac{1}{8} \left[(3\pi + 2sin(2\pi) + \frac{sin(4\pi)}{4}) - (0 + 2sin(0) + \frac{sin(0)}{4})\right]$

Since $sin(n\pi) = 0$ for any integer $n$:

$= \frac{1}{8} (3\pi + 0 + 0 - 0) = \frac{3\pi}{8}$

Integral 2: $\int_{0}^{\pi} sin^{4}x dx$

$sin^{4}x = (sin^{2}x)^{2} = \left(\frac{1-cos(2x)}{2}\right)^{2} = \frac{1-2cos(2x)+cos^{2}(2x)}{4}$

Substitute $cos^{2}(2x) = \frac{1+cos(4x)}{2}$:

$sin^{4}x = \frac{1-2cos(2x)+\frac{1+cos(4x)}{2}}{4} = \frac{2-4cos(2x)+1+cos(4x)}{8} = \frac{3-4cos(2x)+cos(4x)}{8}$

Now, integrate:

$\int_{0}^{\pi} sin^{4}x dx = \int_{0}^{\pi} \frac{3-4cos(2x)+cos(4x)}{8} dx$ $= \frac{1}{8} \left[3x - \frac{4sin(2x)}{2} + \frac{sin(4x)}{4}\right]_{0}^{\pi}$ $= \frac{1}{8} \left[3x - 2sin(2x) + \frac{sin(4x)}{4}\right]_{0}^{\pi}$ $= \frac{1}{8} \left[(3\pi - 2sin(2\pi) + \frac{sin(4\pi)}{4}) - (0 - 2sin(0) + \frac{sin(0)}{4})\right]$ $= \frac{1}{8} (3\pi - 0 + 0 - 0) = \frac{3\pi}{8}$

Integral 3: $\int_{0}^{\pi} cos^{2}x sin^{2}x dx$

$cos^{2}x sin^{2}x = (cos x sin x)^{2} = \left(\frac{sin(2x)}{2}\right)^{2} = \frac{sin^{2}(2x)}{4}$

Substitute $sin^{2}(2x) = \frac{1-cos(4x)}{2}$:

$cos^{2}x sin^{2}x = \frac{1}{4} \left(\frac{1-cos(4x)}{2}\right) = \frac{1-cos(4x)}{8}$

Now, integrate:

$\int_{0}^{\pi} cos^{2}x sin^{2}x dx = \int_{0}^{\pi} \frac{1-cos(4x)}{8} dx$ $= \frac{1}{8} \left[x - \frac{sin(4x)}{4}\right]_{0}^{\pi}$ $= \frac{1}{8} \left[(\pi - \frac{sin(4\pi)}{4}) - (0 - \frac{sin(0)}{4})\right]$ $= \frac{1}{8} (\pi - 0 - 0) = \frac{\pi}{8}$

Step 3: Substitute the evaluated integrals back into the expression for $I$

$I = a^{4}\left(\frac{3\pi}{8}\right) + b^{4}\left(\frac{3\pi}{8}\right) + 2a^{2}b^{2}\left(\frac{\pi}{8}\right)$ $I = \frac{3\pi a^{4}}{8} + \frac{3\pi b^{4}}{8} + \frac{2\pi a^{2}b^{2}}{8}$ $I = \frac{\pi}{8} (3a^{4} + 3b^{4} + 2a^{2}b^{2})$

The final answer is $\frac{\pi}{8}(3a^{4} + 3b^{4} + 2a^{2}b^{2})$.

Solution: The integral is expanded and then each term is integrated using trigonometric identities to reduce powers. The integral can be written as: $I = a^{4}\int_{0}^{\pi} \cos^{4}x dx + b^{4}\int_{0}^{\pi} \sin^{4}x dx + 2a^{2}b^{2}\int_{0}^{\pi} \cos^{2}x \sin^{2}x dx$ Using the identities $\cos^{2}x = \frac{1+\cos(2x)}{2}$, $\sin^{2}x = \frac{1-\cos(2x)}{2}$, and $\sin x \cos x = \frac{\sin(2x)}{2}$:

1. $\int_{0}^{\pi} \cos^{4}x dx = \int_{0}^{\pi} \left(\frac{1+\cos(2x)}{2}\right)^2 dx = \frac{1}{4}\int_{0}^{\pi} (1+2\cos(2x)+\cos^{2}(2x)) dx$ $= \frac{1}{4}\int_{0}^{\pi} \left(1+2\cos(2x)+\frac{1+\cos(4x)}{2}\right) dx = \frac{1}{8}\int_{0}^{\pi} (3+4\cos(2x)+\cos(4x)) dx$ $= \frac{1}{8}\left[3x + 2\sin(2x) + \frac{\sin(4x)}{4}\right]_{0}^{\pi} = \frac{3\pi}{8}$
2. $\int_{0}^{\pi} \sin^{4}x dx = \int_{0}^{\pi} \left(\frac{1-\cos(2x)}{2}\right)^2 dx = \frac{1}{4}\int_{0}^{\pi} (1-2\cos(2x)+\cos^{2}(2x)) dx$ $= \frac{1}{4}\int_{0}^{\pi} \left(1-2\cos(2x)+\frac{1+\cos(4x)}{2}\right) dx = \frac{1}{8}\int_{0}^{\pi} (3-4\cos(2x)+\cos(4x)) dx$ $= \frac{1}{8}\left[3x - 2\sin(2x) + \frac{\sin(4x)}{4}\right]_{0}^{\pi} = \frac{3\pi}{8}$
3. $\int_{0}^{\pi} \cos^{2}x \sin^{2}x dx = \int_{0}^{\pi} \left(\frac{\sin(2x)}{2}\right)^2 dx = \frac{1}{4}\int_{0}^{\pi} \sin^{2}(2x) dx$ $= \frac{1}{4}\int_{0}^{\pi} \frac{1-\cos(4x)}{2} dx = \frac{1}{8}\int_{0}^{\pi} (1-\cos(4x)) dx$ $= \frac{1}{8}\left[x - \frac{\sin(4x)}{4}\right]_{0}^{\pi} = \frac{\pi}{8}$

Substituting these values back into the expression for $I$: $I = a^{4}\left(\frac{3\pi}{8}\right) + b^{4}\left(\frac{3\pi}{8}\right) + 2a^{2}b^{2}\left(\frac{\pi}{8}\right)$ $I = \frac{3\pi a^{4}}{8} + \frac{3\pi b^{4}}{8} + \frac{2\pi a^{2}b^{2}}{8}$ $I = \frac{\pi}{8}(3a^{4} + 3b^{4} + 2a^{2}b^{2})$

Answer: $\frac{\pi}{8}(3a^{4} + 3b^{4} + 2a^{2}b^{2})$