Question

$\int_0^\infty x^{a x} \sin(b x+c)dx$

Answer 1

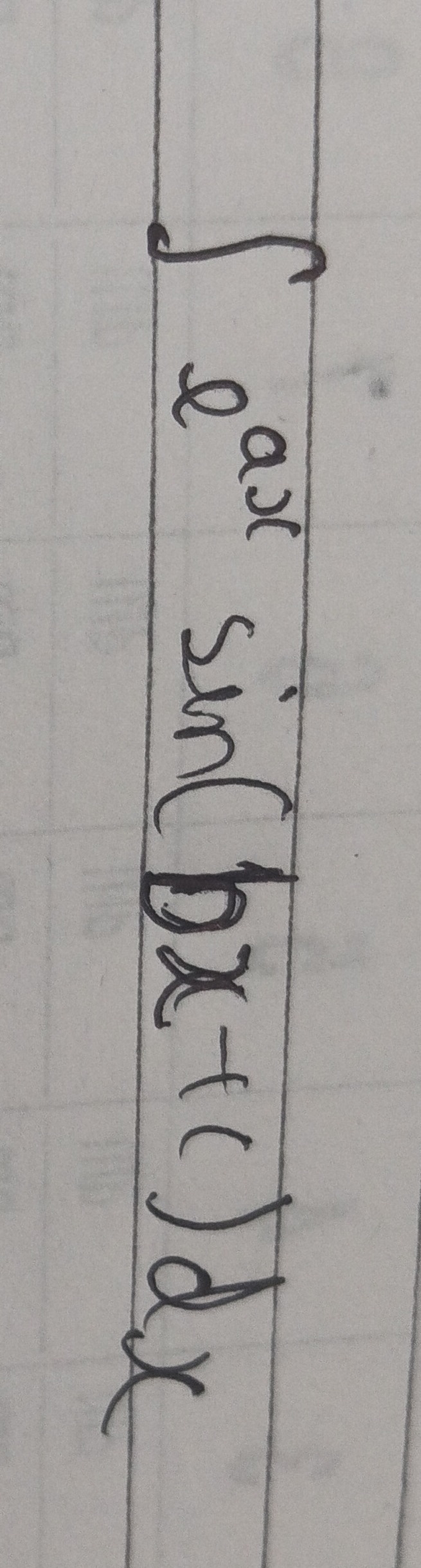
The integral cannot be evaluated in a simple closed form for general a,b,c. It converges only for a < 0.

Answer 2

The given integral is $I = \int_0^\infty x^{a x} \sin(b x+c)dx$.

First, let's analyze the behavior of the integrand $f(x) = x^{ax} \sin(bx+c)$. The term $x^{ax}$ can be rewritten as $e^{ax \ln x}$.

Case 1: $a > 0$

As $x \to \infty$, $ax \ln x \to \infty$. Therefore, $x^{ax} = e^{ax \ln x} \to \infty$. Since the sine term $\sin(bx+c)$ oscillates between -1 and 1, the magnitude of the integrand $|f(x)| = |x^{ax} \sin(bx+c)|$ will grow without bound as $x \to \infty$. For an integral to converge, the integrand must approach zero as $x \to \infty$. Since $x^{ax}$ grows unboundedly, the integral $\int_0^\infty x^{ax} \sin(bx+c)dx$ diverges if $a > 0$.

Case 2: $a = 0$

If $a=0$, the integrand becomes $x^{0 \cdot x} \sin(bx+c) = x^0 \sin(bx+c) = 1 \cdot \sin(bx+c) = \sin(bx+c)$ (assuming $x^0=1$ for $x>0$). The integral becomes $\int_0^\infty \sin(bx+c)dx$. The antiderivative is $-\frac{\cos(bx+c)}{b}$. As $x \to \infty$, $\cos(bx+c)$ oscillates between -1 and 1, so the limit does not exist. Therefore, the integral diverges if $a=0$.

Case 3: $a < 0$

Let $a = -k$ where $k > 0$. The integrand becomes $x^{-kx} \sin(bx+c) = e^{-kx \ln x} \sin(bx+c)$.

• Behavior as $x \to 0^+$:

As $x \to 0^+$, $x \ln x \to 0$. So, $-kx \ln x \to 0$. Thus, $e^{-kx \ln x} \to e^0 = 1$. The integrand approaches $1 \cdot \sin(c) = \sin(c)$ as $x \to 0^+$. The integral is well-behaved at the lower limit $x=0$.

• Behavior as $x \to \infty$:

As $x \to \infty$, $kx \ln x \to \infty$. So, $e^{-kx \ln x} \to 0$. To check for convergence, we can compare $x^{-kx}$ with a known convergent function. For $x \ge e$, we have $\ln x \ge 1$. Therefore, for $x \ge e$, $kx \ln x \ge kx$. This implies $e^{-kx \ln x} \le e^{-kx}$ for $x \ge e$. The integral $\int_e^\infty e^{-kx} dx = \left[ -\frac{1}{k} e^{-kx} \right]_e^\infty = 0 - (-\frac{1}{k} e^{-ke}) = \frac{1}{k} e^{-ke}$, which converges for $k>0$. Since $|x^{-kx} \sin(bx+c)| \le x^{-kx}$, and $\int_e^\infty x^{-kx} dx$ converges by comparison with $\int_e^\infty e^{-kx} dx$, the integral $\int_0^\infty x^{-kx} \sin(bx+c)dx$ converges absolutely if $a<0$.

Conclusion:

The integral $\int_0^\infty x^{a x} \sin(b x+c)dx$ converges only if $a < 0$. However, the question asks to "evaluate" the integral. This typically implies finding a closed-form expression. The integral $\int_0^\infty x^{-kx} \sin(bx+c)dx$ does not have a simple closed-form solution in terms of elementary functions or common special functions typically covered in JEE/NEET syllabus. This integral is generally considered non-elementary. For instance, even the simpler integral $\int_0^\infty x^{-x} dx$ (which corresponds to $k=1, b=0, c=\pi/2$) does not have a simple closed form.

Given the context of JEE/NEET, it is highly improbable that such a complex non-elementary integral is expected to be evaluated. The question might be testing the understanding of convergence criteria or it might be a question out of syllabus. Without specific values for $a, b, c$ that simplify the integral, or a recognition of it being a known advanced result, it cannot be evaluated in a simple form.

If the question is from a multiple-choice context, and options include "diverges," that would be the answer for $a \ge 0$. If it expects an exact value, it's likely a misframed question for this level. Assuming the question expects an evaluation, and no simplification is apparent, it implies the integral does not have a simple solution.

Therefore, the integral does not have a general closed-form solution expressible in elementary functions. It converges only for $a < 0$.