Question

$\int_{0}^{\infty} (\frac{ln \ x}{x^{2} + 2x + 4}) dx$

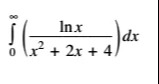
Answer 1

$\frac{\pi \ln 2}{3\sqrt{3}}$

Answer 2

The integral $I = \int_{0}^{\infty} \frac{\ln x}{x^{2} + 2x + 4} dx$ is solved using a property for integrals of the form $\int_{0}^{\infty} \frac{\ln x}{x^2+ax+b} dx$.

1. A substitution $x = b/t$ (here $x=4/t$) is applied to the integral. This transforms the integral into $I = \int_{0}^{\infty} \frac{\ln b - \ln x}{x^2+ax+b} dx$.

2. Adding the original integral and the transformed integral yields $2I = \int_{0}^{\infty} \frac{\ln b}{x^2+ax+b} dx$.

3. This simplifies to $I = \frac{\ln b}{2} \int_{0}^{\infty} \frac{1}{x^2+ax+b} dx$.

4. For the given problem, $a=2, b=4$. So $I = \frac{\ln 4}{2} \int_{0}^{\infty} \frac{1}{x^2+2x+4} dx = \ln 2 \int_{0}^{\infty} \frac{1}{(x+1)^2+3} dx$.

5. The remaining integral is evaluated using a standard arctangent form after a simple substitution $u=x+1$. $\int_{1}^{\infty} \frac{1}{u^2+(\sqrt{3})^2} du = \left[ \frac{1}{\sqrt{3}} \arctan\left(\frac{u}{\sqrt{3}}\right) \right]_{1}^{\infty} = \frac{1}{\sqrt{3}} \left(\frac{\pi}{2} - \frac{\pi}{6}\right) = \frac{1}{\sqrt{3}} \frac{\pi}{3} = \frac{\pi}{3\sqrt{3}}$.

6. Multiplying by $\ln 2$ gives the final result: $\frac{\pi \ln 2}{3\sqrt{3}}$.