Question

$\int_{0}^{\frac{\pi}{2}} \frac{\sqrt{\sin x}}{\sqrt{\sin x} + \sqrt{\cos x}} dx$

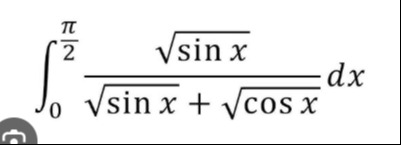
Answer 1

$\frac{\pi}{4}$

Answer 2

1. Substitute $x = \frac{\pi}{2} - u$ to obtain an equivalent integral.

2. Add the original integral and its substitution form to obtain $2I = \frac{\pi}{2}$.

3. Solve for $I$ to get $I = \frac{\pi}{4}$.