Question

$\int_0^4 |2x-5| dx =$

Answer 1

$\frac{17}{2}$

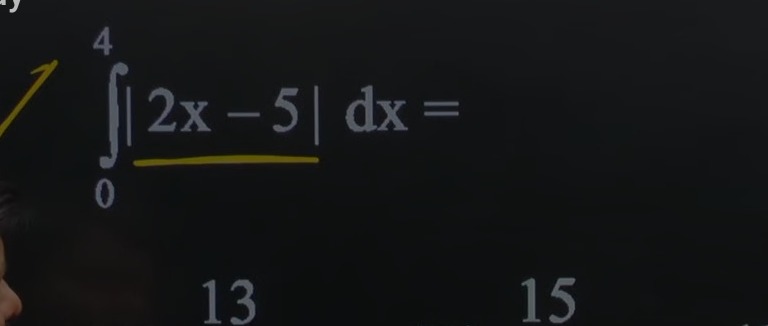
Answer 2

1. Identify the critical point:
   Solve $2x - 5 = 0$ to get $x = \frac{5}{2} = 2.5$.

2. Split the integral:

   $$\int_{0}^{4} |2x-5|\,dx = \int_{0}^{2.5} |2x-5|\,dx + \int_{2.5}^{4} |2x-5|\,dx.$$
   • For $x \in [0, 2.5]$, $2x-5 \le 0$ so $|2x-5| = 5-2x$.
   • For $x \in [2.5, 4]$, $2x-5 \ge 0$ so $|2x-5| = 2x-5$.

3. Evaluate each integral:

   • First integral:

     $$\int_{0}^{2.5} (5-2x) dx = \left[5x - x^2\right]_{0}^{2.5} = \Big(5(2.5) - (2.5)^2\Big) - 0 = 12.5 - 6.25 = 6.25.$$

   • Second integral:

     $$\int_{2.5}^{4} (2x-5) dx = \left[x^2-5x\right]_{2.5}^{4} = \Big((16-20)\Big) - \Big((6.25-12.5)\Big) = (-4) - (-6.25) = 2.25.$$

4. Sum the results:

   $$6.25 + 2.25 = 8.5 = \frac{17}{2}.$$