Question

$\int_0^3 \{x\} dx$

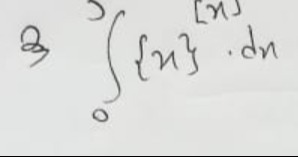
Answer 1

$\frac{3}{2}$

Answer 2

The fractional part function $\{x\}$ is equal to $x - \lfloor x \rfloor$. The integral $\int_0^3 \{x\} dx$ can be evaluated by splitting the interval $[0, 3]$ into subintervals where $\lfloor x \rfloor$ is constant. $\int_0^3 \{x\} dx = \int_0^1 \{x\} dx + \int_1^2 \{x\} dx + \int_2^3 \{x\} dx$ For $x \in [0, 1)$, $\{x\} = x$. For $x \in [1, 2)$, $\{x\} = x-1$. For $x \in [2, 3)$, $\{x\} = x-2$. Substituting these into the integral: $\int_0^1 x dx + \int_1^2 (x-1) dx + \int_2^3 (x-2) dx$ Evaluating each integral: $\int_0^1 x dx = \left[\frac{x^2}{2}\right]_0^1 = \frac{1}{2}$ $\int_1^2 (x-1) dx = \left[\frac{x^2}{2} - x\right]_1^2 = \frac{1}{2}$ $\int_2^3 (x-2) dx = \left[\frac{x^2}{2} - 2x\right]_2^3 = \frac{1}{2}$ Summing the results: $\frac{1}{2} + \frac{1}{2} + \frac{1}{2} = \frac{3}{2}$ Alternatively, the integral represents the area under the graph of $y=\{x\}$ from $x=0$ to $x=3$. This area consists of three triangles, each with base 1 and height 1, so the total area is $3 \times (\frac{1}{2} \times 1 \times 1) = \frac{3}{2}$.