Question

$\int_{0}^{2}x^{2}[x]dx$

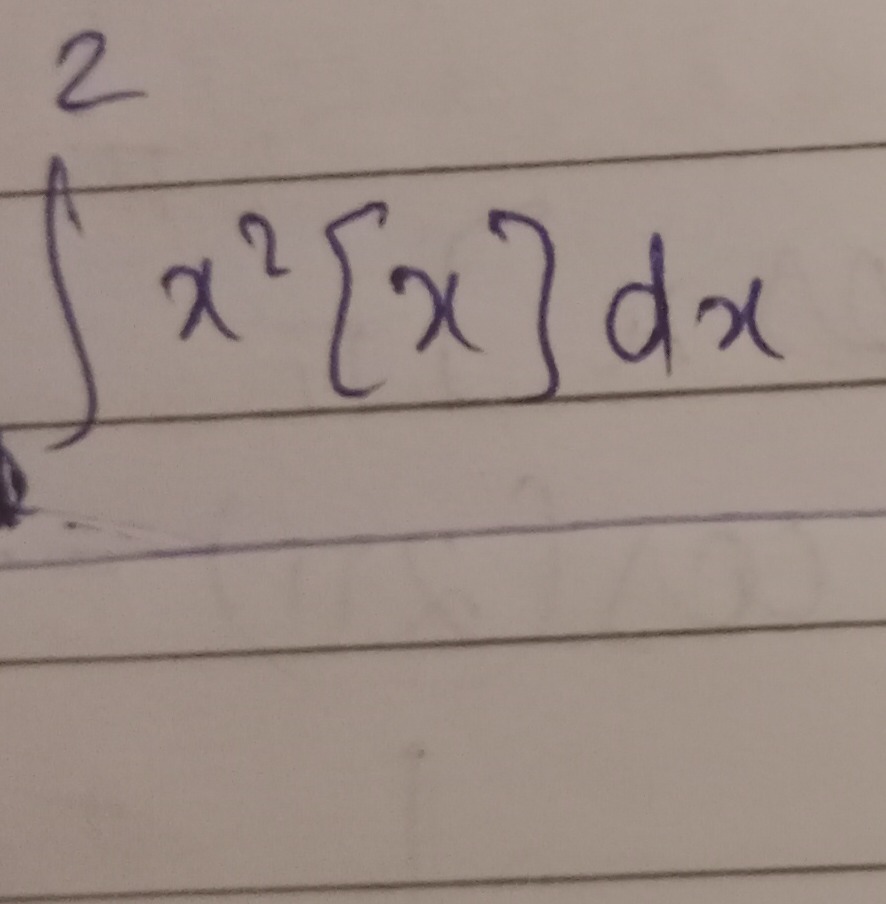
Answer 1

$\frac{7}{3}$

Answer 2

Solution:

Split the integral into intervals over which $[x]$ is constant:

$$\int_{0}^{2} x^2 [x] \,dx = \int_{0}^{1} x^2 \cdot 0 \,dx + \int_{1}^{2} x^2 \cdot 1 \,dx.$$

The first integral is 0. For the second:

$$\int_{1}^{2} x^2 \,dx = \left[\frac{x^3}{3}\right]_1^2 = \frac{8}{3} - \frac{1}{3} = \frac{7}{3}.$$

Thus, the answer is:

$$\frac{7}{3}.$$

Explanation (Minimal):

Break the integration into intervals [0,1] and [1,2]. The integral over [0,1] is 0 (since $[x]=0$). Over [1,2], $[x]=1$, so evaluate $\int_{1}^{2} x^2dx = \frac{7}{3}$.