Solveeit Logo
Login

Question

Question: $\int_{0}^{2\pi} (\sin x+|\sin x|) dx$ is equal to...

∫02π(sin⁡x+∣sin⁡x∣)dx\int_{0}^{2\pi} (\sin x+|\sin x|) dx is equal to

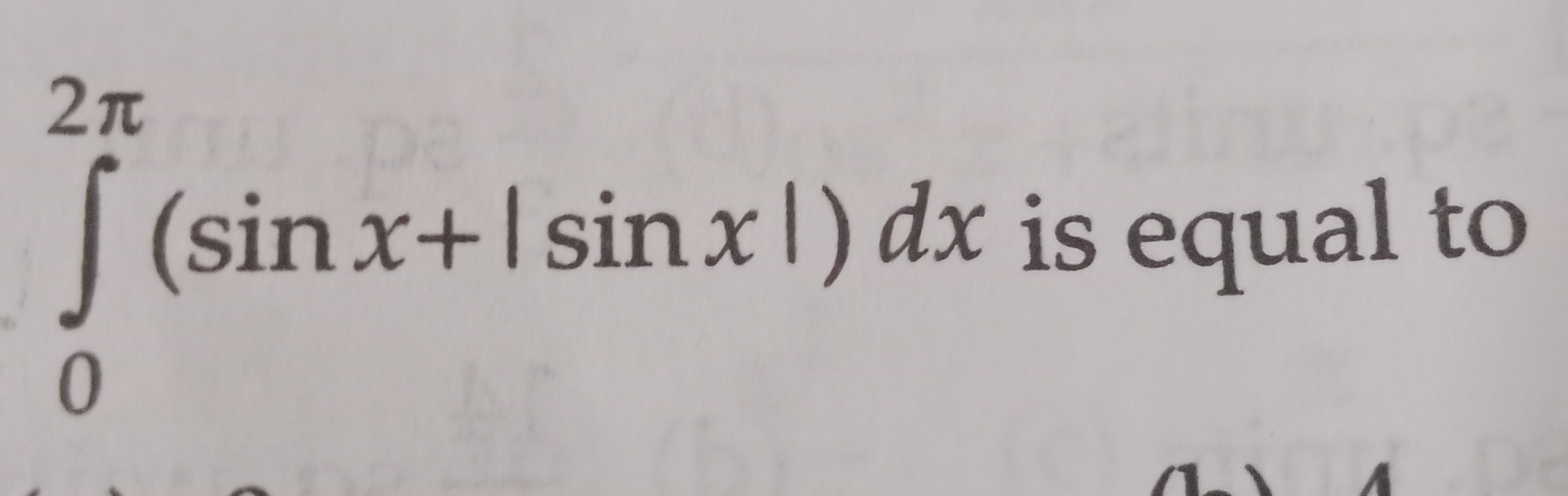
A

0

B

2

C

4

D

None of these

Answer

4

Explanation

Solution

To evaluate the integral ∫02π(sin⁡x+∣sin⁡x∣)dx\int_{0}^{2\pi} (\sin x+|\sin x|) dx, we can split it into two parts:

  1. ∫02πsin⁡x dx\int_{0}^{2\pi} \sin x \, dx
  2. ∫02π∣sin⁡x∣ dx\int_{0}^{2\pi} |\sin x| \, dx

The first integral is: ∫02πsin⁡x dx=[−cos⁡x]02π=−cos⁡(2π)+cos⁡(0)=−1+1=0\int_{0}^{2\pi} \sin x \, dx = [-\cos x]_{0}^{2\pi} = -\cos(2\pi) + \cos(0) = -1 + 1 = 0

For the second integral, we consider the intervals where sin⁡x\sin x is positive and negative. In [0,π][0, \pi], sin⁡x≥0\sin x \ge 0, so ∣sin⁡x∣=sin⁡x|\sin x| = \sin x. In [π,2π][\pi, 2\pi], sin⁡x≤0\sin x \le 0, so ∣sin⁡x∣=−sin⁡x|\sin x| = -\sin x.

Thus, ∫02π∣sin⁡x∣ dx=∫0πsin⁡x dx+∫π2π(−sin⁡x) dx\int_{0}^{2\pi} |\sin x| \, dx = \int_{0}^{\pi} \sin x \, dx + \int_{\pi}^{2\pi} (-\sin x) \, dx

Now, we calculate these integrals: ∫0πsin⁡x dx=[−cos⁡x]0π=−cos⁡(π)+cos⁡(0)=−(−1)+1=2\int_{0}^{\pi} \sin x \, dx = [-\cos x]_{0}^{\pi} = -\cos(\pi) + \cos(0) = -(-1) + 1 = 2 ∫π2π(−sin⁡x) dx=[cos⁡x]π2π=cos⁡(2π)−cos⁡(π)=1−(−1)=2\int_{\pi}^{2\pi} (-\sin x) \, dx = [\cos x]_{\pi}^{2\pi} = \cos(2\pi) - \cos(\pi) = 1 - (-1) = 2

So, ∫02π∣sin⁡x∣ dx=2+2=4\int_{0}^{2\pi} |\sin x| \, dx = 2 + 2 = 4

Finally, we combine the results: ∫02π(sin⁡x+∣sin⁡x∣)dx=0+4=4\int_{0}^{2\pi} (\sin x+|\sin x|) dx = 0 + 4 = 4