Question

$\int_{0}^{1/2} cos^{-1}(x) dx$

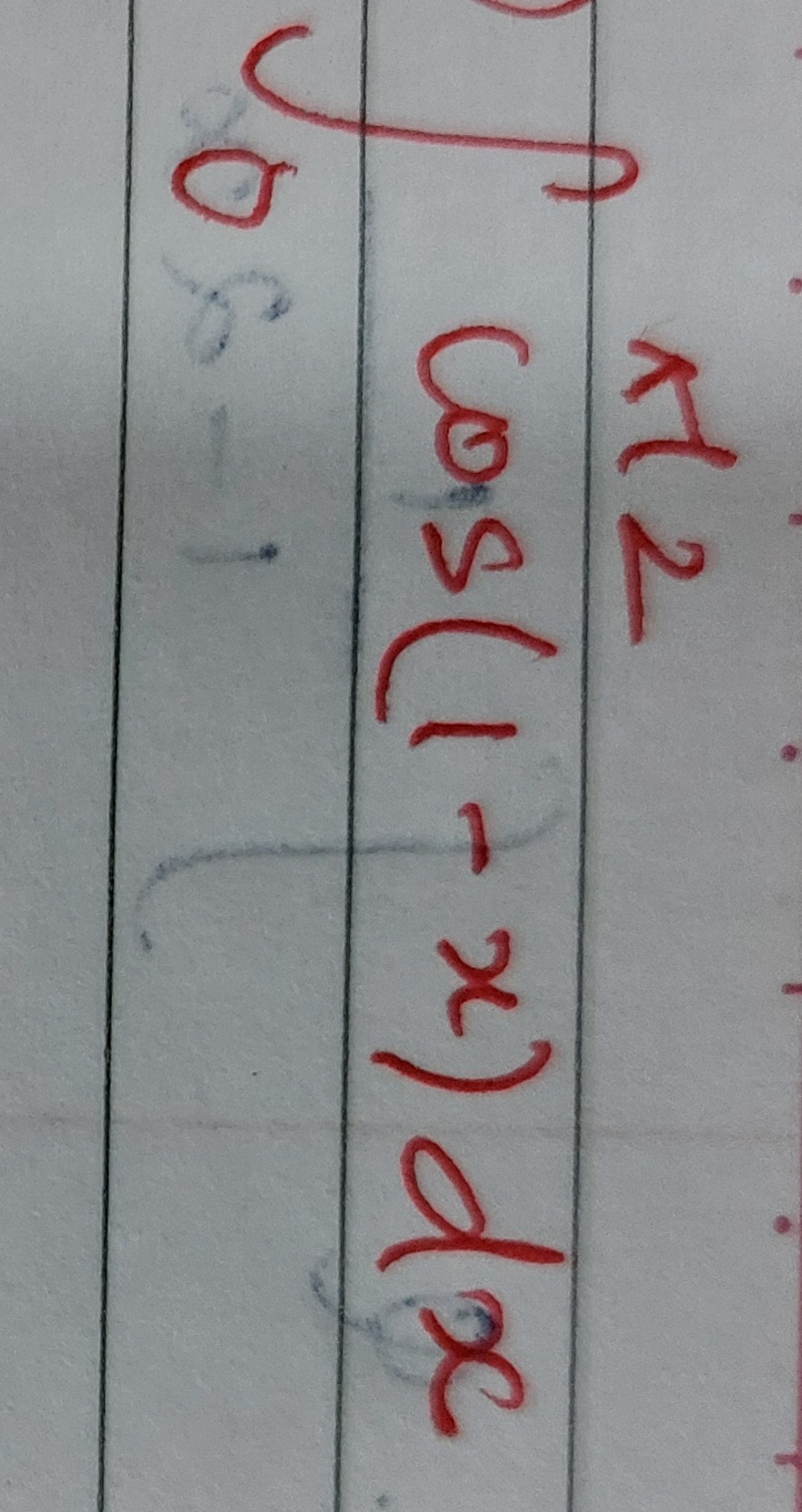
Answer 1

$\frac{\pi}{6}+1-\frac{\sqrt{3}}{2}$

Answer 2

We evaluate the integral

$I=\int_{0}^{1/2}\cos^{-1}(x)dx$.

Step 1: Integration by Parts

Let

$u=\cos^{-1}(x), dv=dx$.

Then,

$du=-\frac{1}{\sqrt{1-x^2}}dx, v=x$.

Thus,

$I=\left[x\cos^{-1}(x)\right]_0^{1/2}+\int_0^{1/2} \frac{x}{\sqrt{1-x^2}}dx$.

Step 2: Evaluate the Boundary Term

At $x=\frac{1}{2}$, $\cos^{-1}\frac{1}{2}=\frac{\pi}{3}$ and at $x=0$, $\cos^{-1}(0)=\frac{\pi}{2}$ but multiplied by 0 gives 0:

$\left[x\cos^{-1}(x)\right]_0^{1/2}=\frac{1}{2}\cdot\frac{\pi}{3}-0=\frac{\pi}{6}$.

Step 3: Evaluate the Integral $\displaystyle \int_0^{1/2} \frac{x}{\sqrt{1-x^2}}dx$

Use the substitution:

$w=1-x^2, dw=-2x\,dx\Rightarrow x\,dx=-\frac{dw}{2}$.

When $x=0,\ w=1$; when $x=\frac{1}{2},\ w=1-\frac{1}{4}=\frac{3}{4}$. The integral becomes:

$\int_0^{1/2}\frac{x}{\sqrt{1-x^2}}dx = -\frac{1}{2}\int_{1}^{3/4}w^{-1/2}dw$.

Changing the limits order gives:

$-\frac{1}{2}\int_{1}^{3/4}w^{-1/2}dw=\frac{1}{2}\int_{3/4}^{1}w^{-1/2}dw$.

Now integrate:

$\int w^{-1/2}dw=2w^{1/2}$,

thus,

$\frac{1}{2}\left[2w^{1/2}\right]_{w=3/4}^{1}=\left[w^{1/2}\right]_{3/4}^{1}=1-\sqrt{\frac{3}{4}}=1-\frac{\sqrt{3}}{2}$.

Step 4: Combine the Results

$I=\frac{\pi}{6}+1-\frac{\sqrt{3}}{2}$.