Solveeit Logo
Login

Question

Question: $\int_{0}^{1} \ln(x+\frac{1}{y}) dy - \int_{0}^{1} \ln(\frac{x^2+1}{y^2}) dy + \int_{0}^{1} \ln(1-y)...

∫01ln⁡(x+1y)dy−∫01ln⁡(x2+1y2)dy+∫01ln⁡(1−y)dy.\int_{0}^{1} \ln(x+\frac{1}{y}) dy - \int_{0}^{1} \ln(\frac{x^2+1}{y^2}) dy + \int_{0}^{1} \ln(1-y) dy.

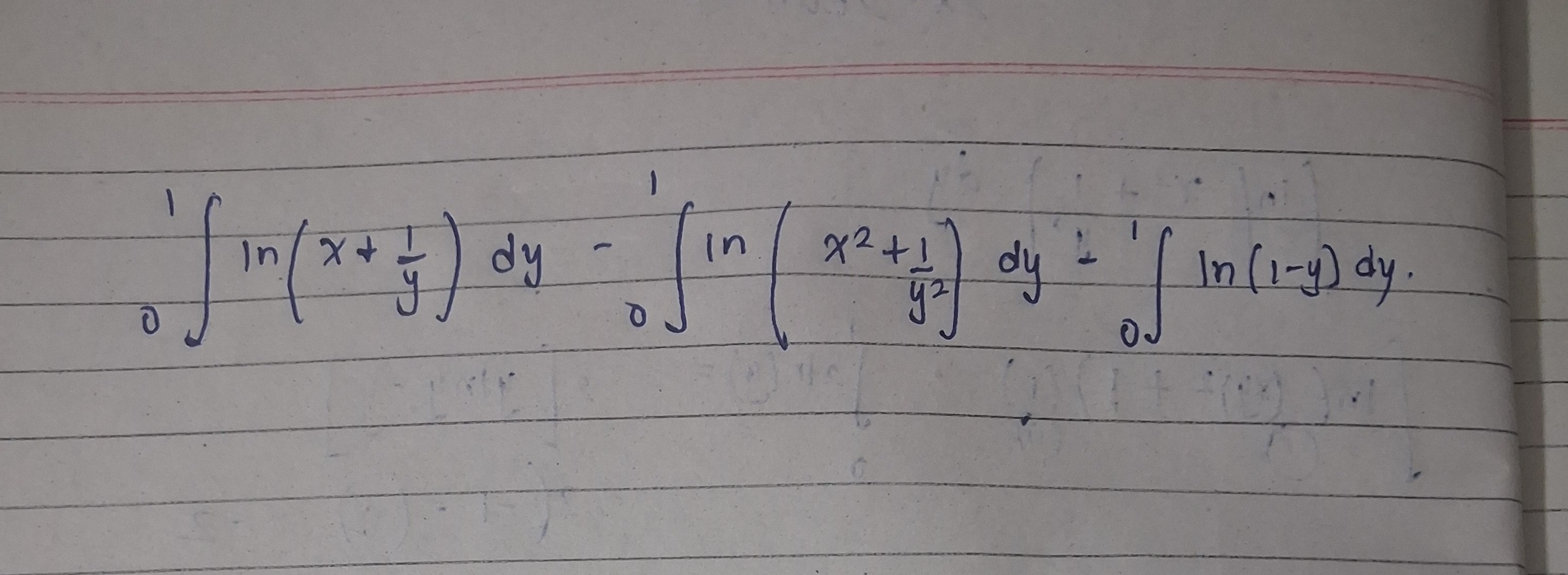
Answer

x+1xln⁡(x+1)−ln⁡(x2+1)−3\frac{x+1}{x}\ln(x+1) - \ln(x^2+1) - 3

Explanation

Solution

The problem involves evaluating a definite integral expression. The strategy is to combine the three integrals into a single integral using logarithm properties. Then, the integrand is decomposed into simpler logarithmic terms. Each of these simpler integrals is evaluated, paying attention to improper integrals at the limits. Finally, the results of the individual integrals are combined to obtain the final expression in terms of xx.

The key steps are:

  1. Combine the three integrals into one: ∫01ln⁡(y(xy+1)(1−y)x2+1)dy\int_{0}^{1} \ln\left( \frac{y(xy+1)(1-y)}{x^2+1} \right) dy.
  2. Expand using logarithm properties: ∫01(ln⁡y+ln⁡(xy+1)+ln⁡(1−y)−ln⁡(x2+1))dy\int_{0}^{1} (\ln y + \ln(xy+1) + \ln(1-y) - \ln(x^2+1)) dy.
  3. Evaluate each term:
    • ∫01ln⁡y dy=−1\int_{0}^{1} \ln y \, dy = -1.
    • ∫01ln⁡(1−y) dy=−1\int_{0}^{1} \ln(1-y) \, dy = -1.
    • ∫01ln⁡(x2+1) dy=ln⁡(x2+1)\int_{0}^{1} \ln(x^2+1) \, dy = \ln(x^2+1).
    • ∫01ln⁡(xy+1) dy=x+1xln⁡(x+1)−1\int_{0}^{1} \ln(xy+1) \, dy = \frac{x+1}{x}\ln(x+1) - 1.
  4. Sum the results: (−1)+(x+1xln⁡(x+1)−1)+(−1)−ln⁡(x2+1)=x+1xln⁡(x+1)−ln⁡(x2+1)−3(-1) + (\frac{x+1}{x}\ln(x+1) - 1) + (-1) - \ln(x^2+1) = \frac{x+1}{x}\ln(x+1) - \ln(x^2+1) - 3.