Question

$\int_{0}^{1} \frac{\sqrt{1+x^{2}}}{1+x^{3}}dx$

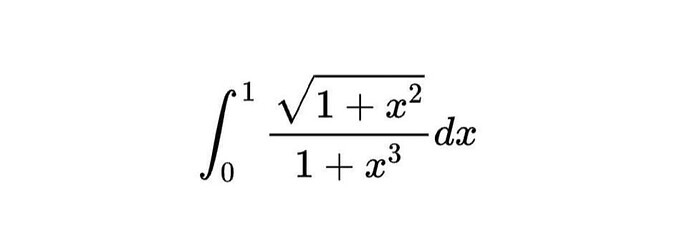
Answer 1

No option provided

Answer 2

The problem integral $I = \int_{0}^{1} \frac{\sqrt{1+x^{2}}}{1+x^{3}}dx$ is evaluated by applying the substitution $x = \frac{1}{t}$. This transformation leads to $I = \int_{1}^{\infty} \frac{\sqrt{1+t^{2}}}{1+t^{3}}dt$. This means the integral from 0 to 1 is equal to the integral from 1 to infinity. While this property is insightful, the numerical evaluation of this integral requires advanced techniques (like complex analysis or special functions) which are beyond the scope of JEE/NEET syllabus. Therefore, this integral cannot be solved by typical methods taught for these exams.