Question

$\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} e^{x} \cdot (1 - \cot(x) + \cot^{2}(x))dx$

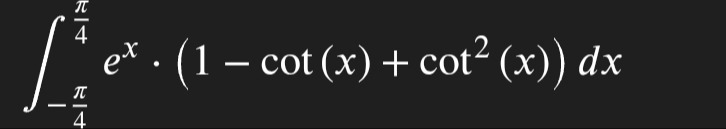
Answer 1

$-(e^{\frac{\pi}{4}} + e^{-\frac{\pi}{4}})$

Answer 2

The integrand $e^{x} (1 - \cot(x) + \cot^{2}(x))$ simplifies to $e^{x} (\csc^{2}(x) - \cot(x))$ using $1 + \cot^{2}(x) = \csc^{2}(x)$.

This is of the form $e^x (f'(x) + f(x))$ where $f(x) = -\cot(x)$ and $f'(x) = \csc^2(x)$.

The integral of this form is $e^x f(x)$.

So, the antiderivative is $-e^x \cot(x)$.

Evaluating from $-\frac{\pi}{4}$ to $\frac{\pi}{4}$:

$\left[ -e^x \cot(x) \right]_{-\frac{\pi}{4}}^{\frac{\pi}{4}} = (-e^{\frac{\pi}{4}} \cot(\frac{\pi}{4})) - (-e^{-\frac{\pi}{4}} \cot(-\frac{\pi}{4}))$

$= (-e^{\frac{\pi}{4}} \cdot 1) - (-e^{-\frac{\pi}{4}} \cdot (-1))$

$= -e^{\frac{\pi}{4}} - e^{-\frac{\pi}{4}} = -(e^{\frac{\pi}{4}} + e^{-\frac{\pi}{4}})$.