Question

$\int_{-1}^{1} \frac{\cos x}{1+e^{1/x}} dx = ?$

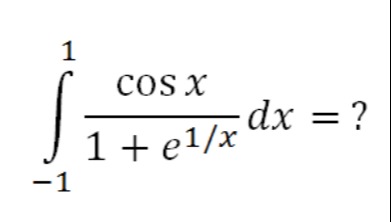
Answer 1

$\sin 1$

Answer 2

Let

$I=\int_{-1}^{1}\frac{\cos x}{1+e^{\frac{1}{x}}}\,dx$.

Define

$f(x)=\frac{\cos x}{1+e^{1/x}}$.

Make the substitution $x\to -x$. Then, we have:

$f(-x)=\frac{\cos(-x)}{1+e^{1/(-x)}}=\frac{\cos x}{1+e^{-1/x}}$.

Now, add the two:

$f(x)+f(-x)=\frac{\cos x}{1+e^{1/x}}+\frac{\cos x}{1+e^{-1/x}}=\cos x\left( \frac{1}{1+e^{1/x}}+\frac{1}{1+e^{-1/x}}\right)$.

Notice that for any real number $z$, it holds that:

$\frac{1}{1+e^{z}}+\frac{1}{1+e^{-z}}=1$.

Thus,

$f(x)+f(-x)=\cos x$.

Changing the order of integration (using the symmetry about 0), we get:

$I=\int_{-1}^{1}f(x)\,dx=\int_{0}^{1}\Big[f(x)+f(-x)\Big]\,dx =\int_{0}^{1}\cos x\,dx$.

Now, evaluate the integral:

$\int_{0}^{1}\cos x\,dx=\sin x\Big|_{0}^{1}=\sin 1-\sin 0=\sin 1$.