Question
Question: $\int \sqrt{\frac{1+2\tan x}{(\sec x + \tan x)}} dx$...
∫(secx+tanx)1+2tanxdx
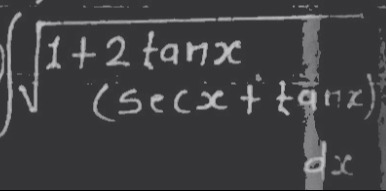
A
∫secx+tanxdx
B
∫secx−tanxdx
C
∫1+sinxcosx+2sinxdx
D
∫secx−tanx1−2tanxdx
Answer
∫1+sinxcosx+2sinxdx
Explanation
Solution
To simplify the integral ∫(secx+tanx)1+2tanxdx, we first rewrite the trigonometric functions in terms of sinx and cosx: tanx=cosxsinx,secx=cosx1 Substitute these into the expression inside the square root: secx+tanx1+2tanx=cosx1+cosxsinx1+2cosxsinx Multiply the numerator and the denominator by cosx: =cosx(cosx1+cosxsinx)cosx(1+2cosxsinx)=1+sinxcosx+2sinx Therefore, the integral can be rewritten as: ∫1+sinxcosx+2sinxdx
