Question
Question: $\int \sin^3 x.\cos^6 x \, dx =$...
∫sin3x.cos6xdx=
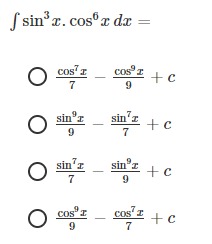
7cos7x−9cos9x+c
9sin9x−7sin7x+c
7sin7x−9sin9x+c
9cos9x−7cos7x+c
9cos9x−7cos7x+c
Solution
The integral to be solved is ∫sin3x.cos6xdx.
We can rewrite the integrand as: ∫sin2x⋅cos6x⋅sinxdx
Using the identity sin2x=1−cos2x, we substitute it into the integral: ∫(1−cos2x)⋅cos6x⋅sinxdx
Now, let's use the substitution method. Let u=cosx. Then, differentiate both sides with respect to x: du=−sinxdx This implies sinxdx=−du.
Substitute u=cosx and sinxdx=−du into the integral: ∫(1−u2)⋅u6⋅(−du) =−∫(u6−u2⋅u6)du =−∫(u6−u8)du
Distribute the negative sign: =∫(u8−u6)du
Now, integrate term by term using the power rule for integration, ∫xndx=n+1xn+1+C: =8+1u8+1−6+1u6+1+C =9u9−7u7+C
Finally, substitute back u=cosx: =9cos9x−7cos7x+C
Comparing this result with the given options, it matches the fourth option.
