Solveeit Logo
Login

Question

Question: $\int sin 2x cos^7x dx$...

∫sin2xcos7xdx\int sin 2x cos^7x dx

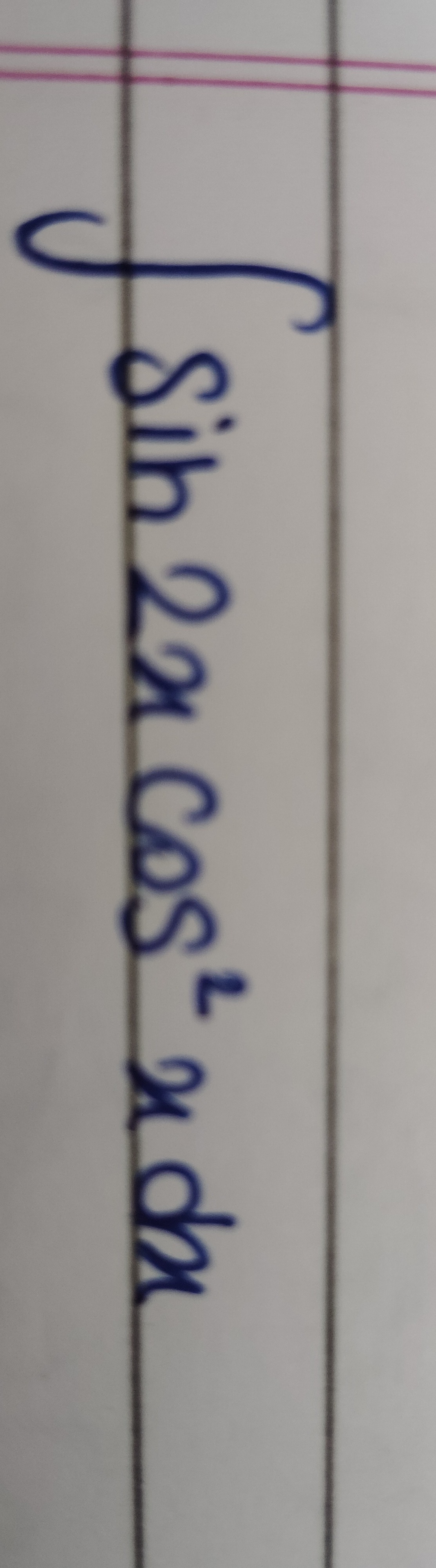
Answer

−29cos⁡9x+C-\frac{2}{9} \cos^9x + C

Explanation

Solution

To solve the integral ∫sin⁡2xcos⁡7x dx\int \sin 2x \cos^7x \, dx, we will use trigonometric identities and substitution.

  1. Use the double angle identity for sine:

    We know that sin⁡2x=2sin⁡xcos⁡x\sin 2x = 2 \sin x \cos x. Substitute this into the integral:

    ∫sin⁡2xcos⁡7x dx=∫(2sin⁡xcos⁡x)cos⁡7x dx\int \sin 2x \cos^7x \, dx = \int (2 \sin x \cos x) \cos^7x \, dx =∫2sin⁡xcos⁡8x dx= \int 2 \sin x \cos^8x \, dx

  2. Use substitution:

    Let u=cos⁡xu = \cos x. Then, differentiate uu with respect to xx:

    dudx=−sin⁡x\frac{du}{dx} = -\sin x

    So, du=−sin⁡x dxdu = -\sin x \, dx, which implies sin⁡x dx=−du\sin x \, dx = -du.

  3. Substitute uu and dudu into the integral:

    ∫2cos⁡8x(sin⁡x dx)=∫2u8(−du)\int 2 \cos^8x (\sin x \, dx) = \int 2 u^8 (-du) =−2∫u8 du= -2 \int u^8 \, du

  4. Integrate with respect to uu:

    Using the power rule for integration, ∫un du=un+1n+1+C\int u^n \, du = \frac{u^{n+1}}{n+1} + C:

    −2∫u8 du=−2(u8+18+1)+C-2 \int u^8 \, du = -2 \left( \frac{u^{8+1}}{8+1} \right) + C =−2(u99)+C= -2 \left( \frac{u^9}{9} \right) + C =−29u9+C= -\frac{2}{9} u^9 + C

  5. Substitute back u=cos⁡xu = \cos x:

    −29cos⁡9x+C-\frac{2}{9} \cos^9x + C

The final answer is −29cos⁡9x+C-\frac{2}{9} \cos^9x + C.