Question

$\int sec^3x dx$

Answer 1

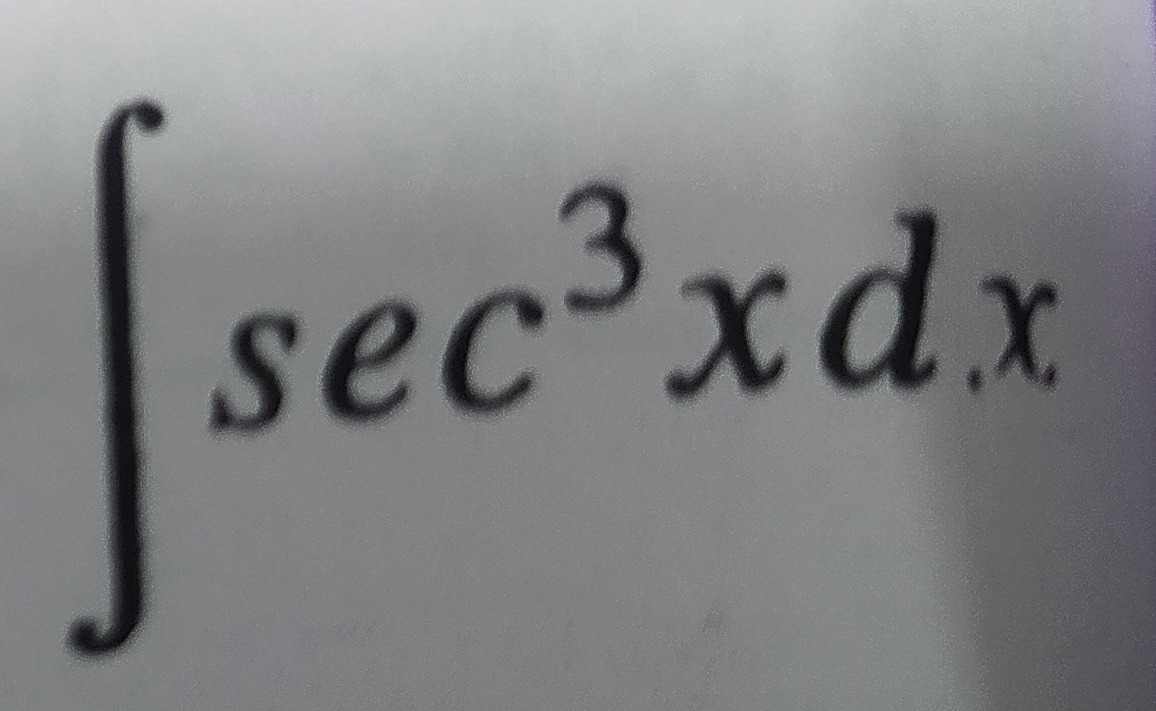
$\frac{1}{2}(\sec x \tan x + \ln|\sec x + \tan x|) + C$

Answer 2

The integral $\int \sec^3 x \, dx$ is a standard integral solved using integration by parts.

Let $I = \int \sec^3 x \, dx$. We can rewrite $\sec^3 x$ as $\sec x \cdot \sec^2 x$. Apply integration by parts, $\int u \, dv = uv - \int v \, du$. Let $u = \sec x$ and $dv = \sec^2 x \, dx$. Then, $du = \frac{d}{dx}(\sec x) \, dx = \sec x \tan x \, dx$. And, $v = \int \sec^2 x \, dx = \tan x$.

Substitute these into the integration by parts formula: $I = \sec x \tan x - \int \tan x (\sec x \tan x) \, dx$ $I = \sec x \tan x - \int \sec x \tan^2 x \, dx$

Now, use the trigonometric identity $\tan^2 x = \sec^2 x - 1$: $I = \sec x \tan x - \int \sec x (\sec^2 x - 1) \, dx$ $I = \sec x \tan x - \int (\sec^3 x - \sec x) \, dx$ $I = \sec x \tan x - \int \sec^3 x \, dx + \int \sec x \, dx$

Notice that the integral $\int \sec^3 x \, dx$ is $I$. Substitute $I$ back into the equation: $I = \sec x \tan x - I + \int \sec x \, dx$

We know the standard integral of $\sec x$: $\int \sec x \, dx = \ln|\sec x + \tan x| + C_1$

Substitute this back into the equation: $I = \sec x \tan x - I + \ln|\sec x + \tan x|$

Now, solve for $I$: $2I = \sec x \tan x + \ln|\sec x + \tan x|$ $I = \frac{1}{2} (\sec x \tan x + \ln|\sec x + \tan x|) + C$ (where $C = C_1/2$ is the constant of integration)