Question
Question: $\int \sec^2(2-3x)dx$...
∫sec2(2−3x)dx
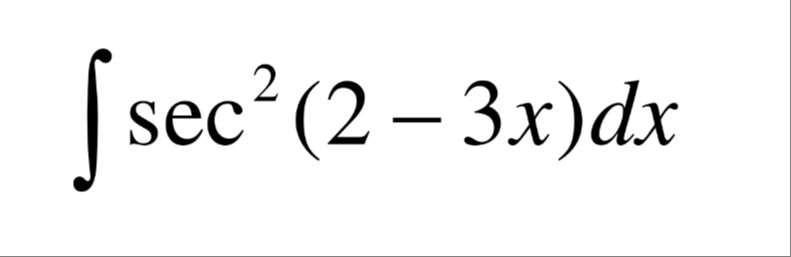
Answer
−31tan(2−3x)+C
Explanation
Solution
Let u=2−3x, so du=−3dx, which means dx=−31du. The integral becomes −31∫sec2(u)du=−31tan(u)+C=−31tan(2−3x)+C
∫sec2(2−3x)dx
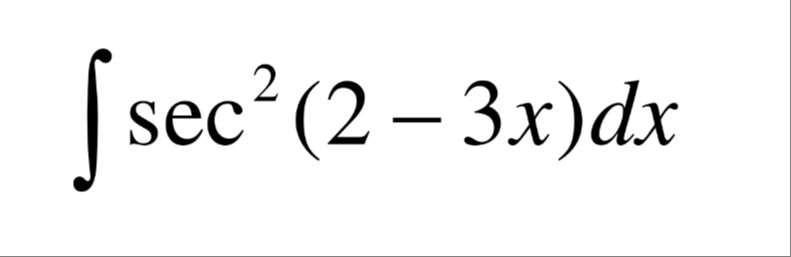
−31tan(2−3x)+C
Let u=2−3x, so du=−3dx, which means dx=−31du. The integral becomes −31∫sec2(u)du=−31tan(u)+C=−31tan(2−3x)+C