Question

\int \operatorname{arccot}\left(\frac{1}{\sqrt{1-x^{2}}}\right) d x

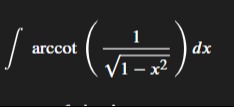
Answer 1

x \arctan\left(\sqrt{1-x^{2}}\right) - \arcsin x + \sqrt{2} \arctan\left(\frac{x}{\sqrt{2(1-x^2)}}\right) + C

Answer 2

First, simplify the integrand using the identity $\operatorname{arccot}(y) = \arctan(1/y)$ for $y>0$: $\operatorname{arccot}\left(\frac{1}{\sqrt{1-x^{2}}}\right) = \arctan\left(\sqrt{1-x^{2}}\right)$ So the integral becomes $\int \arctan\left(\sqrt{1-x^{2}}\right) d x$.

Use integration by parts with $u = \arctan\left(\sqrt{1-x^{2}}\right)$ and $dv = dx$. Then $v = x$ and $du = \frac{-x}{(2-x^2)\sqrt{1-x^2}} dx$. $\int \arctan\left(\sqrt{1-x^{2}}\right) d x = x \arctan\left(\sqrt{1-x^{2}}\right) - \int x \cdot \frac{-x}{(2-x^2)\sqrt{1-x^2}} dx$ $= x \arctan\left(\sqrt{1-x^{2}}\right) + \int \frac{x^2}{(2-x^2)\sqrt{1-x^2}} dx$ Let $I_1 = \int \frac{x^2}{(2-x^2)\sqrt{1-x^2}} dx$. Substitute $x = \sin\theta$, $dx = \cos\theta d\theta$. $I_1 = \int \frac{\sin^2\theta}{1+\cos^2\theta} d\theta = -\theta + \sqrt{2} \arctan\left(\frac{\tan\theta}{\sqrt{2}}\right)$ Substituting back $x = \sin\theta$: $I_1 = -\arcsin x + \sqrt{2} \arctan\left(\frac{x}{\sqrt{2(1-x^2)}}\right)$ Combining the terms: $\int \arctan\left(\sqrt{1-x^{2}}\right) d x = x \arctan\left(\sqrt{1-x^{2}}\right) - \arcsin x + \sqrt{2} \arctan\left(\frac{x}{\sqrt{2(1-x^2)}}\right) + C$