Question
Question: $\int \left( \frac{2^x-5^x}{10^x} \right) dx$ is equal to...
∫(10x2x−5x)dx is equal to
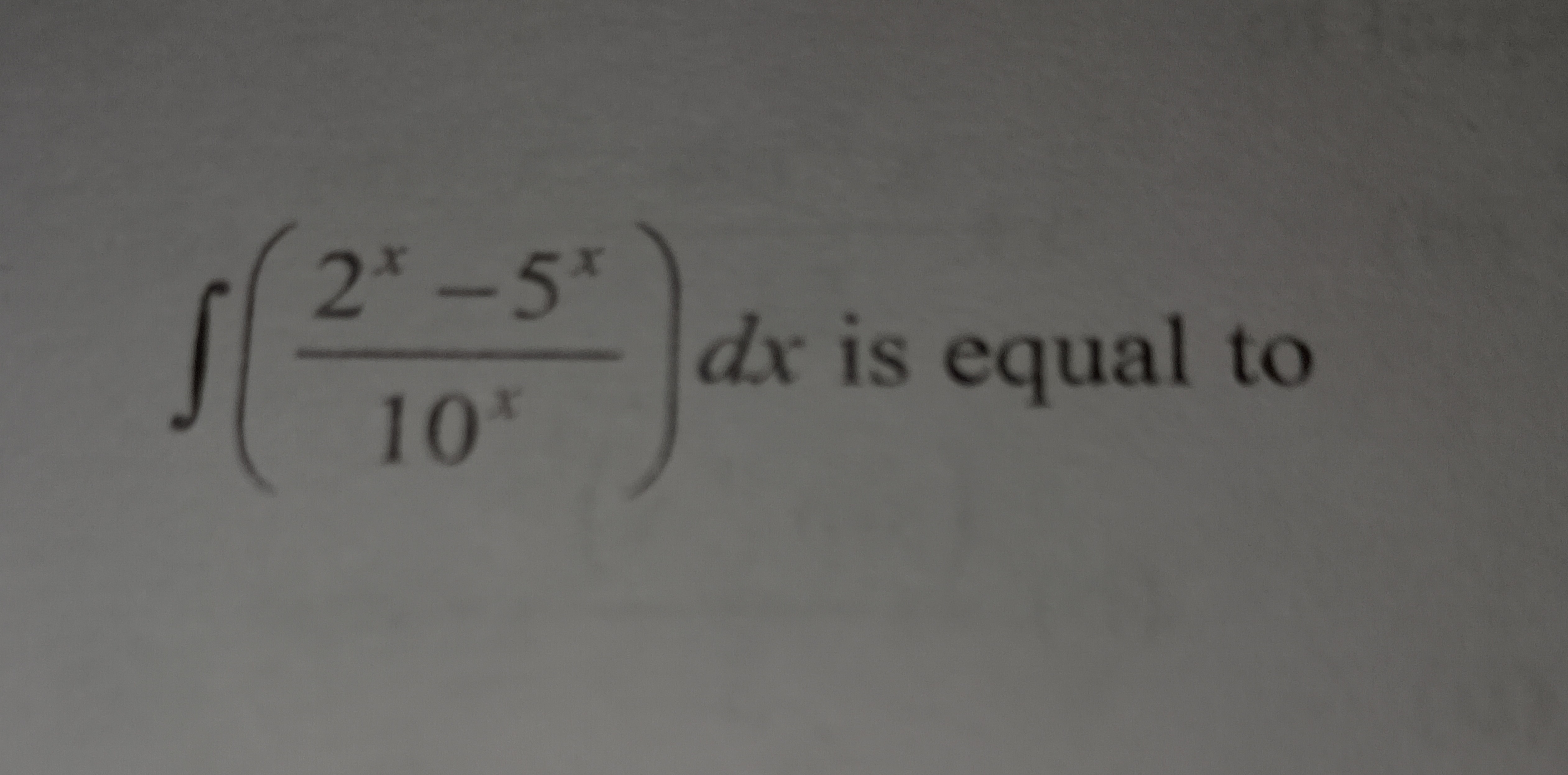
ln22−x−ln55−x+C
Solution
The problem asks us to evaluate the indefinite integral ∫(10x2x−5x)dx.
Step-by-step solution:
-
Split the integrand: The fraction can be split into two separate terms: 10x2x−5x=10x2x−10x5x
-
Simplify each term using exponent rules: Recall that bxax=(ba)x. 10x2x=(102)x=(51)x=5−x 10x5x=(105)x=(21)x=2−x
-
Rewrite the integral: Substitute the simplified terms back into the integral: ∫(10x2x−5x)dx=∫(5−x−2−x)dx
-
Integrate each term: We use the standard integration formula for exponential functions: ∫akxdx=klnaakx+C.
-
For the first term, ∫5−xdx: Here a=5 and k=−1. ∫5−xdx=(−1)ln55−x=−ln55−x
-
For the second term, ∫2−xdx: Here a=2 and k=−1. ∫2−xdx=(−1)ln22−x=−ln22−x
-
-
Combine the results: ∫(5−x−2−x)dx=(−ln55−x)−(−ln22−x)+C =−ln55−x+ln22−x+C Rearranging the terms to have the positive term first: =ln22−x−ln55−x+C This can also be written in terms of positive exponents: =2xln21−5xln51+C
The final answer is ln22−x−ln55−x+C.
Explanation: The integral is simplified by splitting the fraction and using exponent rules. Each resulting term is of the form akx, which is integrated using the standard formula ∫akxdx=klnaakx.
Answer: The integral is equal to ln22−x−ln55−x+C.
