Solveeit Logo
Login

Question

Question: $\int \frac{x^{6}-1}{x^{2}+1}dx$...

∫x6−1x2+1dx\int \frac{x^{6}-1}{x^{2}+1}dx

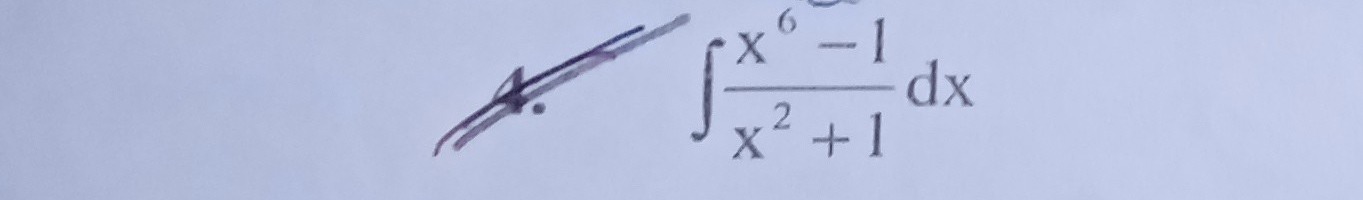
Answer

x55−x33+x−2arctan⁡x+C\frac{x^5}{5} - \frac{x^3}{3} + x - 2\arctan x + C

Explanation

Solution

Perform polynomial long division to write

x6−1x2+1=x4−x2+1−2x2+1.\frac{x^6-1}{x^2+1} = x^4 - x^2 + 1 - \frac{2}{x^2+1}.

Thus, the integral becomes

∫x6−1x2+1 dx=∫(x4−x2+1)dx−2∫1x2+1dx=x55−x33+x−2arctan⁡x+C.\begin{aligned} \int \frac{x^6-1}{x^2+1}\,dx &= \int \left(x^4 - x^2 + 1\right)dx - 2\int \frac{1}{x^2+1}dx\\[2mm] &= \frac{x^5}{5} - \frac{x^3}{3} + x - 2\arctan x + C. \end{aligned}

Core Explanation:

  1. Divide x6−1x^6-1 by x2+1x^2+1 to get x4−x2+1−2x2+1x^4-x^2+1 - \frac{2}{x^2+1}.

  2. Integrate each term separately.