Question
Question: $\int \frac{(x^4 - x)^{1/4}}{x^5} dx$ is equal to...
∫x5(x4−x)1/4dx is equal to
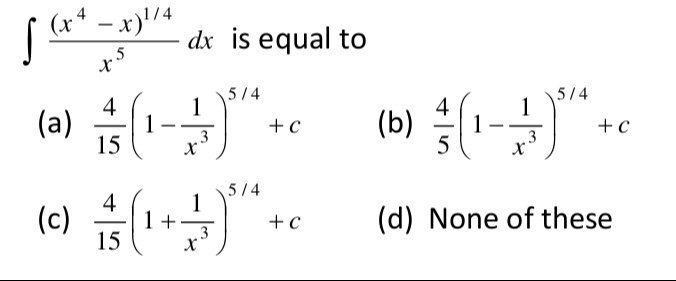
154(1−x31)5/4+c
54(1−x31)5/4+c
154(1+x31)5/4+c
None of these
154(1−x31)5/4+c
Solution
The integral to evaluate is I=∫x5(x4−x)1/4dx.
We can factor out x4 from the term inside the parenthesis in the numerator: (x4−x)1/4=(x4(1−x4x))1/4=(x4(1−x31))1/4.
Using the property (ab)n=anbn, we get: (x4(1−x31))1/4=(x4)1/4(1−x31)1/4.
For real numbers, (x4)1/4=∣x∣.
So the integral becomes I=∫x5∣x∣(1−x31)1/4dx.
For the expression (x4−x)1/4 to be a real number, we must have x4−x≥0. x4−x=x(x3−1)=x(x−1)(x2+x+1). The quadratic factor x2+x+1=(x+1/2)2+3/4 is always positive. So x(x−1)(x2+x+1)≥0 implies x(x−1)≥0. This inequality holds for x≤0 or x≥1.
Let's consider the case where x≥1. In this case, x>0, so ∣x∣=x. The integral becomes I=∫x5x(1−x31)1/4dx=∫x4(1−x31)1/4dx. Let u=1−x31. Then du=dxd(1−x−3)dx=(0−(−3)x−4)dx=3x−4dx=x43dx. So, x41dx=31du. Substituting this into the integral: I=∫u1/4⋅31du=31∫u1/4du. Using the power rule for integration, ∫undu=n+1un+1+C (for n=−1): I=311/4+1u1/4+1+C=31⋅5/4u5/4+C. I=31⋅54u5/4+C=154u5/4+C. Substitute back u=1−x31: I=154(1−x31)5/4+C. This result is valid for x≥1.
