Question

$\int \frac{x^3}{\sqrt{x^2+2}} dx =$

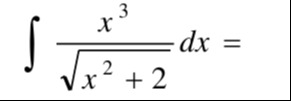
Answer 1

$\frac{1}{3} (x^2-4) \sqrt{x^2+2} + C$

Answer 2

To solve the integral $\int \frac{x^3}{\sqrt{x^2+2}} dx$, we use substitution.

1. Substitution: Let $u = x^2 + 2$, then $du = 2x \, dx$ and $x^2 = u - 2$.

2. Rewrite the integral: $\int \frac{x^3}{\sqrt{x^2+2}} dx = \int \frac{x^2 \cdot x}{\sqrt{x^2+2}} dx = \int \frac{(u-2)}{\sqrt{u}} \cdot \frac{1}{2} du = \frac{1}{2} \int \frac{u-2}{\sqrt{u}} du$

3. Simplify: $\frac{1}{2} \int \frac{u-2}{\sqrt{u}} du = \frac{1}{2} \int (u^{1/2} - 2u^{-1/2}) du$

4. Integrate: $\frac{1}{2} \int (u^{1/2} - 2u^{-1/2}) du = \frac{1}{2} \left( \frac{2}{3}u^{3/2} - 4u^{1/2} \right) + C = \frac{1}{3}u^{3/2} - 2u^{1/2} + C$

5. Substitute back: $\frac{1}{3}u^{3/2} - 2u^{1/2} + C = \frac{1}{3}(x^2+2)^{3/2} - 2(x^2+2)^{1/2} + C$

6. Factor and simplify: $\frac{1}{3}(x^2+2)^{3/2} - 2(x^2+2)^{1/2} + C = (x^2+2)^{1/2} \left[ \frac{1}{3}(x^2+2) - 2 \right] + C = \sqrt{x^2+2} \left[ \frac{x^2+2-6}{3} \right] + C = \frac{1}{3}(x^2-4)\sqrt{x^2+2} + C$

Thus, the integral evaluates to $\frac{1}{3} (x^2-4) \sqrt{x^2+2} + C$.