Question

$\int \frac{x^2 + 2x}{x^2 + 2x + 1} dx$

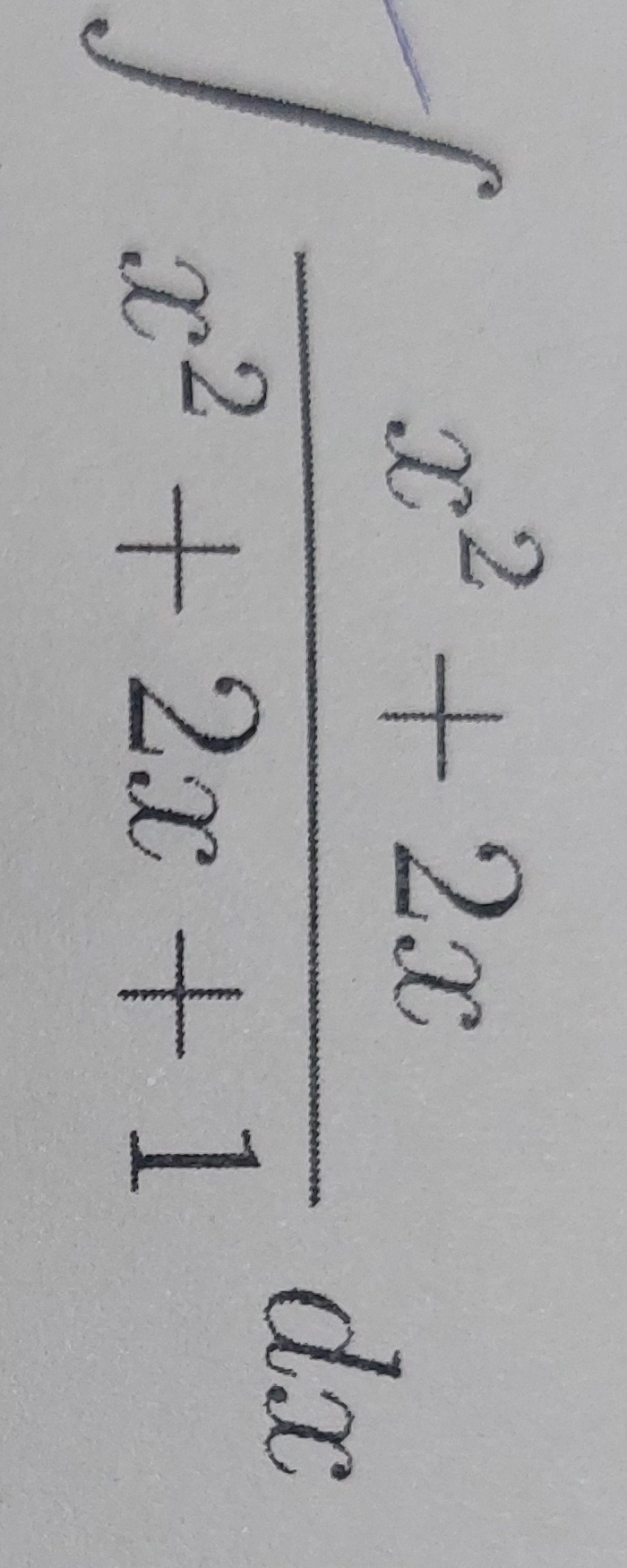
Answer 1

$x + \frac{1}{x+1} + C$

Answer 2

Solution:

Notice that

$$x^2 + 2x = (x+1)^2 - 1.$$

Thus,

$$\frac{x^2 + 2x}{x^2 + 2x + 1} = \frac{(x+1)^2 - 1}{(x+1)^2} = 1 - \frac{1}{(x+1)^2}.$$

The integral becomes:

$$\int \left(1 - \frac{1}{(x+1)^2}\right) dx = \int 1\, dx - \int \frac{1}{(x+1)^2}\, dx.$$

Integrate each part:

$$\int 1\, dx = x,$$

and letting $u=x+1$ (so $du=dx$):

$$\int \frac{1}{(x+1)^2}\,dx = \int \frac{1}{u^2}\,du = -\frac{1}{u} = -\frac{1}{x+1}.$$

Thus, the integral is:

$$x - \left(-\frac{1}{x+1}\right) = x + \frac{1}{x+1} + C.$$

---

Explanation (minimal):

Rewrite numerator as $(x+1)^2-1$. Split into $1 - \frac{1}{(x+1)^2}$ and integrate term by term.