Question

$\int \frac{tan x. sec^2x}{4x} .dx$

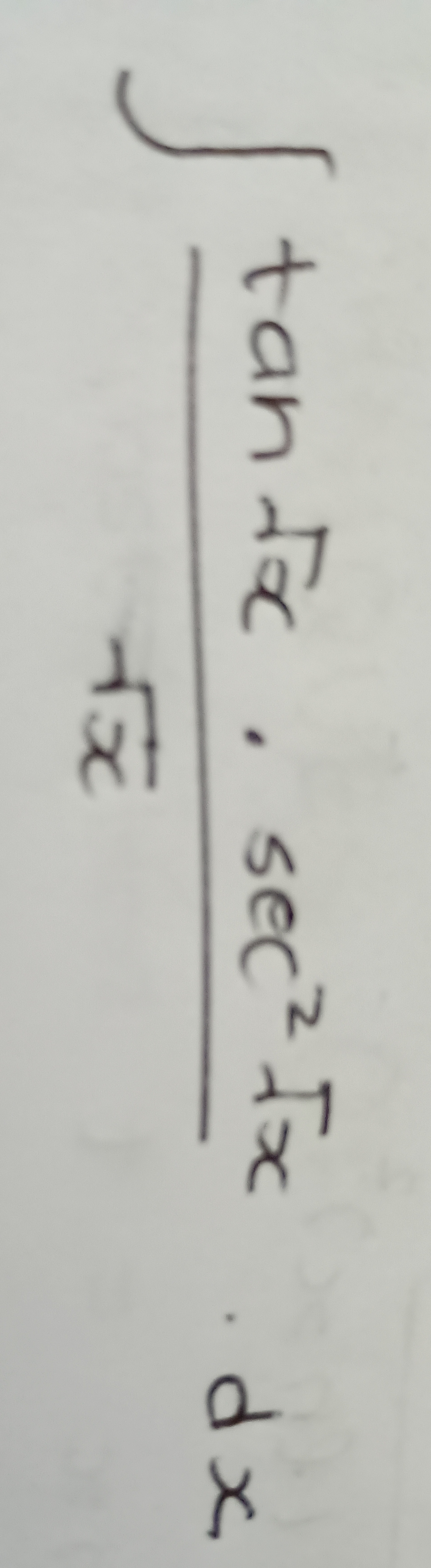
Answer 1

The integral cannot be expressed in terms of elementary functions.

Answer 2

The given integral $\int \frac{\tan x \cdot \sec^2 x}{4x} dx$ is analyzed. The numerator $\tan x \cdot \sec^2 x$ is the derivative of $\frac{1}{2}\tan^2 x$. Applying integration by parts or substitution (e.g., $u=\tan x$) leads to new integrals that still involve $x$ in the denominator in a way that prevents simplification to elementary functions. Specifically, the integral reduces to forms like $\frac{\tan^2 x}{8x} + \frac{1}{8} \int \frac{\tan^2 x}{x^2} dx$, where $\int \frac{\tan^2 x}{x^2} dx$ is non-elementary. Therefore, the integral is non-elementary.