Question
Question: $\int \frac{\sqrt{x+1}+\sqrt{x}}{dx}$...
∫dxx+1+x
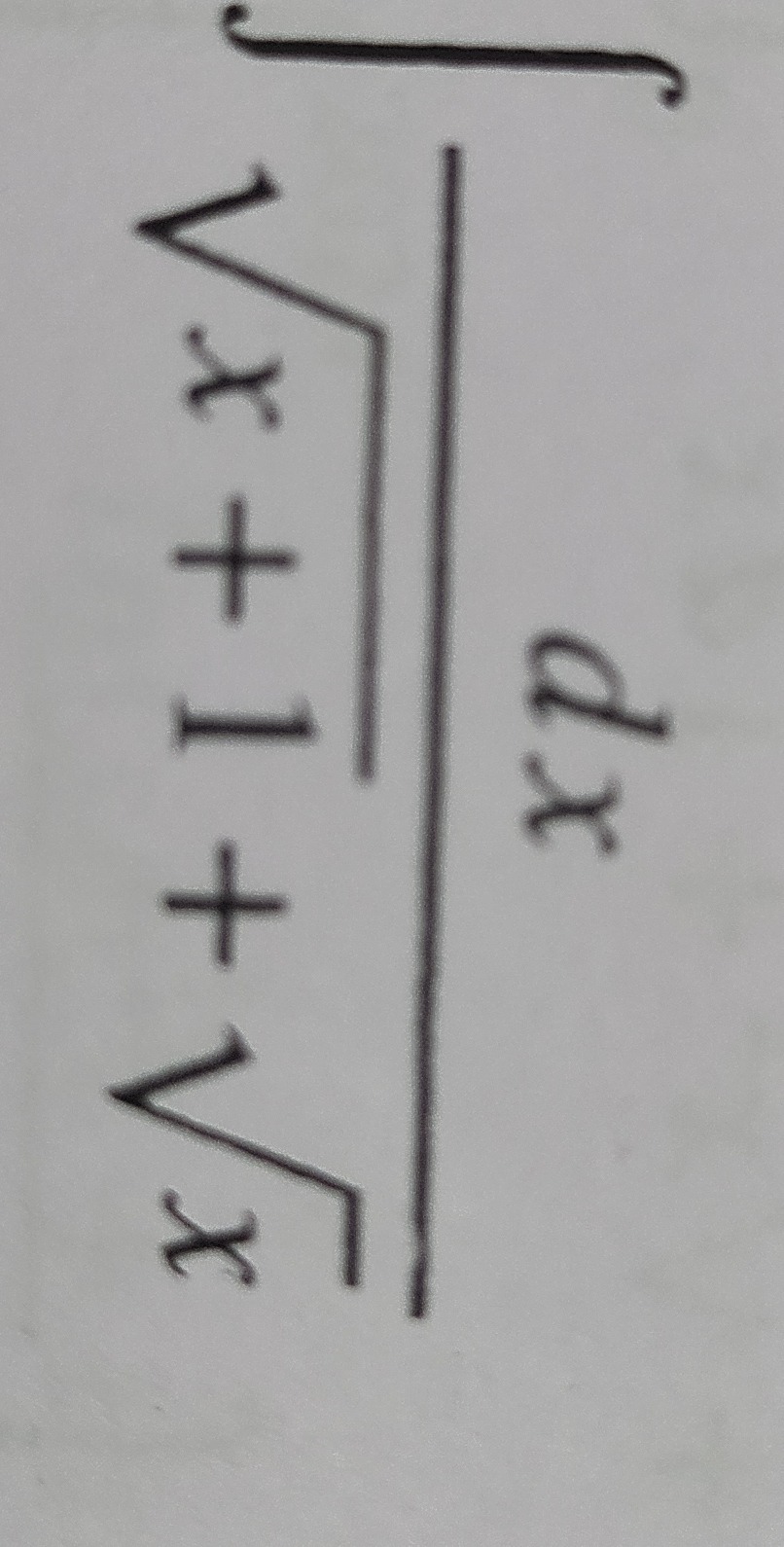
Answer
32(x+1)3/2+32x3/2+C
Explanation
Solution
The problem asks to evaluate the indefinite integral of the sum of two square root functions.
We need to evaluate ∫(x+1+x)dx.
Using the linearity property of integrals, we can split this into two separate integrals:
∫(x+1+x)dx=∫x+1dx+∫xdxNow, let's evaluate each integral:
-
For ∫xdx:
∫x1/2dx=1/2+1x1/2+1+C1=3/2x3/2+C1=32x3/2+C1
Rewrite x as x1/2.
Using the power rule for integration, ∫undu=n+1un+1+C: -
For ∫x+1dx:
∫(x+1)1/2dx=1⋅(1/2+1)(x+1)1/2+1+C2=3/2(x+1)3/2+C2=32(x+1)3/2+C2
Rewrite x+1 as (x+1)1/2.
This is of the form ∫(ax+b)ndx. For a=1, b=1, and n=1/2, we use the generalized power rule: ∫(ax+b)ndx=a(n+1)(ax+b)n+1+C.
Combining the results from both integrals:
∫(x+1+x)dx=32(x+1)3/2+32x3/2+Cwhere C=C1+C2 is the constant of integration.
