Question
Question: $\int \frac{\sqrt{x+1}}{\sqrt{x+1}+\sqrt{x}} dx$...
∫x+1+xx+1dx
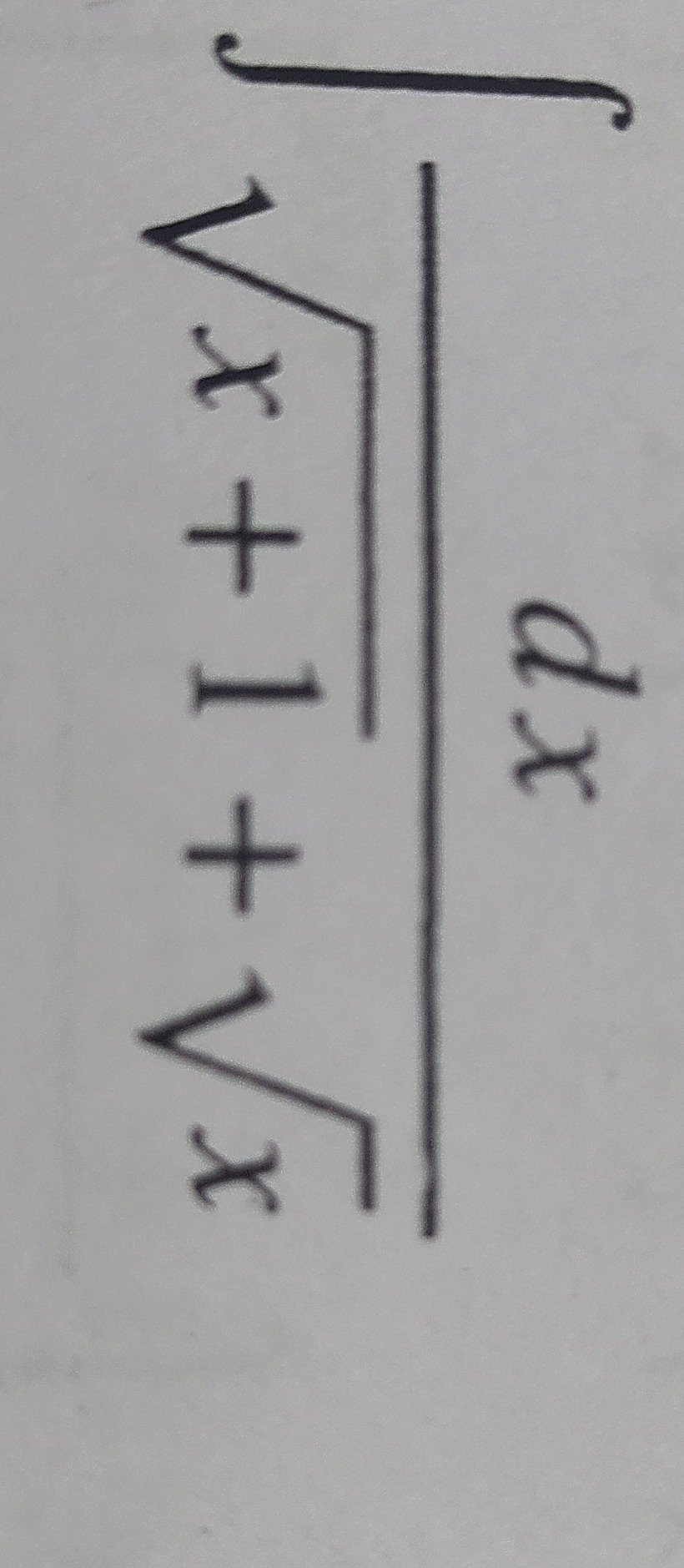
2x2+x−42x+1x2+x+81lnx+21+x2+x+C
Solution
To evaluate the integral ∫x+1+xx+1dx, we can use the technique of rationalizing the denominator.
1. Rationalize the Denominator:
Multiply the numerator and the denominator by the conjugate of the denominator, which is (x+1−x):
I=∫x+1+xx+1×x+1−xx+1−xdx
The denominator becomes a difference of squares:
(x+1)2−(x)2=(x+1)−x=1
The numerator becomes:
x+1(x+1−x)=(x+1)2−x+1x=(x+1)−x(x+1)
So the integral simplifies to:
I=∫1(x+1)−x(x+1)dx
I=∫(x+1)dx−∫x2+xdx
2. Evaluate the First Part of the Integral:
The first part is a simple polynomial integral:
∫(x+1)dx=2x2+x+C1
3. Evaluate the Second Part of the Integral:
The second part is ∫x2+xdx. To solve this, we complete the square inside the square root:
x2+x=x2+2(21)x+(21)2−(21)2=(x+21)2−(21)2
Let u=x+21, then du=dx. Let a=21. The integral becomes:
∫u2−a2du
Using the standard integration formula ∫u2−a2du=2uu2−a2−2a2ln∣u+u2−a2∣+C2:
Substitute back u=x+21 and a=21:
∫x2+xdx=2x+21(x+21)2−(21)2−2(21)2lnx+21+(x+21)2−(21)2+C2
=42x+1x2+x−21/4lnx+21+x2+x+C2
=42x+1x2+x−81lnx+21+x2+x+C2
4. Combine the Results:
Substitute the results from step 2 and step 3 back into the expression for I:
I=(2x2+x)−(42x+1x2+x−81lnx+21+x2+x)+C
I=2x2+x−42x+1x2+x+81lnx+21+x2+x+C
where C=C1−C2 is the constant of integration.
The final answer is 2x2+x−42x+1x2+x+81lnx+21+x2+x+C.
Explanation of the solution:
The integral is solved by rationalizing the denominator, which simplifies the integrand into two parts: a simple polynomial and a square root of a quadratic expression. The polynomial part is integrated directly using the power rule. The quadratic expression under the square root is integrated by completing the square and applying the standard integral formula for ∫u2−a2du.
Answer:
The integral is 2x2+x−42x+1x2+x+81lnx+21+x2+x+C.
