Solveeit Logo
Login

Question

Question: $\int \frac{(\sqrt{x}+1)dx}{\sqrt{x}(\sqrt[3]{x}+1)}$...

∫(x+1)dxx(x3+1)\int \frac{(\sqrt{x}+1)dx}{\sqrt{x}(\sqrt[3]{x}+1)}

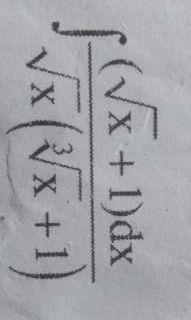
Answer

\frac{3}{2}x^{2/3}-3x^{1/3}+6x^{1/6}+3\ln\Bigl|x^{1/3}+1\Bigr|-6\arctan\Bigl(x^{1/6}\Bigr)+C.

Explanation

Solution

Solution Explanation

We wish to evaluate

I=∫(x+1) dxx (x3+1).I=\int\frac{(\sqrt{x}+1)\,dx}{\sqrt{x}\,(\sqrt[3]{x}+1)}.

Step 1. Make the substitution

t=x1/6⇒x=t6,dx=6t5 dt.t=x^{1/6}\quad\Rightarrow\quad x=t^6,\quad dx=6t^5\,dt.

Note that

x=x1/2=t3,x3=x1/3=t2.\sqrt{x}=x^{1/2}=t^3,\qquad \sqrt[3]{x}=x^{1/3}=t^2.

Step 2. Rewrite the integrand in terms of tt:

I=∫(t3+1)(6t5 dt)t3 (t2+1)=  6∫t5(t3+1)t3(t2+1) dt=  6∫t2(t3+1)t2+1 dt.I=\int\frac{(t^3+1)(6t^5\,dt)}{t^3\,(t^2+1)} =\;6\int\frac{t^5(t^3+1)}{t^3(t^2+1)}\,dt =\;6\int\frac{t^2(t^3+1)}{t^2+1}\,dt.

Step 3. Write the numerator:

t2(t3+1)=t5+t2.t^2(t^3+1)=t^5+t^2.

We now divide t5+t2t^5+t^2 by t2+1t^2+1 using polynomial long division.

Divide: t5+t2t^5+t^2 by t2+1t^2+1

• First, t5÷t2=t3t^5 \div t^2=t^3. Multiply: t3(t2+1)=t5+t3t^3(t^2+1)=t^5+t^3. Subtract:

(t5+t2)−(t5+t3)=−t3+t2.(t^5+t^2) - (t^5+t^3) = -t^3+t^2.

• Next, −t3÷t2=−t-t^3\div t^2=-t. Multiply: −t(t2+1)=−t3−t-t(t^2+1)=-t^3-t. Subtract:

(−t3+t2)−(−t3−t)=t2+t.(-t^3+t^2) - (-t^3-t)=t^2+t.

• Then, t2÷t2=1t^2\div t^2=1. Multiply: 1⋅(t2+1)=t2+11\cdot (t^2+1)=t^2+1. Subtract:

(t2+t)−(t2+1)=t−1.(t^2+t)-(t^2+1)=t-1.

Thus,

t5+t2t2+1=t3−t+1+t−1t2+1.\frac{t^5+t^2}{t^2+1}=t^3-t+1+\frac{t-1}{t^2+1}.

Step 4. Express the integral as

I=6∫[t3−t+1+t−1t2+1]dt.I=6\int\left[t^3-t+1+\frac{t-1}{t^2+1}\right]dt.

Integrate term‑by‑term:

• ∫t3 dt=t44\displaystyle \int t^3\, dt=\frac{t^4}{4}.

• ∫(−t) dt=−t22\displaystyle \int(-t)\, dt=-\frac{t^2}{2}.

• ∫1 dt=t\displaystyle \int1\, dt=t.

• For ∫t−1t2+1 dt\displaystyle \int\frac{t-1}{t^2+1}\,dt, break it as

∫tt2+1 dt−∫1t2+1 dt.\int\frac{t}{t^2+1}\,dt-\int\frac{1}{t^2+1}\,dt.

Now,

∫tt2+1dt=12ln⁡∣t2+1∣,∫1t2+1dt=arctan⁡t.\int\frac{t}{t^2+1}dt=\frac{1}{2}\ln|t^2+1|,\quad \int\frac{1}{t^2+1}dt=\arctan t.

Thus,

∫t−1t2+1 dt=12ln⁡∣t2+1∣−arctan⁡t.\int\frac{t-1}{t^2+1}\,dt=\frac{1}{2}\ln|t^2+1|-\arctan t.

Step 5. Collecting results, we have:

I=6[t44−t22+t+12ln⁡∣t2+1∣−arctan⁡t]+C.I=6\left[\frac{t^4}{4}-\frac{t^2}{2}+t+\frac{1}{2}\ln|t^2+1|-\arctan t\right]+C.

Simplify:

I=32t4−3t2+6t+3ln⁡∣t2+1∣−6arctan⁡t+C.I=\frac{3}{2}t^4-3t^2+6t+3\ln|t^2+1|-6\arctan t+C.

Recall that t=x1/6t=x^{1/6}, so:

t4=x4/6=x2/3,t2=x2/6=x1/3,t=x1/6.t^4=x^{4/6}=x^{2/3},\quad t^2=x^{2/6}=x^{1/3},\quad t=x^{1/6}.

Thus the answer is:

I=32x2/3−3x1/3+6x1/6+3ln⁡∣x1/3+1∣−6arctan⁡(x1/6)+C.\boxed{I=\frac{3}{2}x^{2/3}-3x^{1/3}+6x^{1/6}+3\ln\Bigl|x^{1/3}+1\Bigr|-6\arctan\Bigl(x^{1/6}\Bigr)+C.}

Answer

32x2/3−3x1/3+6x1/6+3ln⁡∣x1/3+1∣−6arctan⁡(x1/6)+C.\frac{3}{2}x^{2/3}-3x^{1/3}+6x^{1/6}+3\ln\Bigl|x^{1/3}+1\Bigr|-6\arctan\Bigl(x^{1/6}\Bigr)+C.