Question

$\int \frac{\sqrt[3]{x^2}+\sqrt[6]{x}}{x(1+\sqrt[3]{x})} dx =$

Answer 1

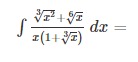
6\sqrt[6]{x} + \ln|x| - 3\ln(1+\sqrt[3]{x}) - 6\arctan(\sqrt[6]{x}) + C

Answer 2

To evaluate the integral $\int \frac{\sqrt[3]{x^2}+\sqrt[6]{x}}{x(1+\sqrt[3]{x})} dx$, we first rewrite the terms using fractional exponents:

$\sqrt[3]{x^2} = x^{2/3}$

$\sqrt[6]{x} = x^{1/6}$

$\sqrt[3]{x} = x^{1/3}$

The integral becomes:

$\int \frac{x^{2/3} + x^{1/6}}{x(1+x^{1/3})} dx$

To eliminate the fractional exponents, we make a substitution. The least common multiple (LCM) of the denominators of the exponents (3, 6, 1, 3) is 6.

Let $x = t^6$. Then, $dx = 6t^5 dt$.

Substitute $x=t^6$ into the integral:

$x^{2/3} = (t^6)^{2/3} = t^4$

$x^{1/6} = (t^6)^{1/6} = t$

$x^{1/3} = (t^6)^{1/3} = t^2$

The integral transforms to:

$\int \frac{t^4 + t}{t^6(1+t^2)} (6t^5 dt)$

Factor out $t$ from the numerator and simplify:

$= \int \frac{t(t^3 + 1)}{t^6(1+t^2)} (6t^5 dt)$

Cancel $t^5$ from $t^6$ in the denominator and $t$ from the numerator:

$= \int \frac{t(t^3 + 1)}{t(1+t^2)} (6 dt)$

$= \int \frac{6(t^3 + 1)}{t(1+t^2)} dt$

The integrand is a rational function. The degree of the numerator ($t^3$) is equal to the degree of the denominator ($t(1+t^2) = t^3+t$). Perform polynomial long division:

$\frac{6t^3+6}{t^3+t} = \frac{6(t^3+t) - 6t + 6}{t^3+t} = 6 + \frac{6-6t}{t^3+t}$

So the integral becomes:

$\int \left( 6 + \frac{6-6t}{t(1+t^2)} \right) dt = \int 6 dt + \int \frac{6-6t}{t(1+t^2)} dt = 6t + \int \frac{6-6t}{t(1+t^2)} dt$

Now, we decompose the remaining fraction $\frac{6-6t}{t(1+t^2)}$ into partial fractions:

$\frac{6-6t}{t(1+t^2)} = \frac{A}{t} + \frac{Bt+C}{1+t^2}$

Multiply both sides by $t(1+t^2)$:

$6-6t = A(1+t^2) + (Bt+C)t$

$6-6t = A + At^2 + Bt^2 + Ct$

$6-6t = (A+B)t^2 + Ct + A$

Comparing coefficients:

Constant term: $A = 6$

Coefficient of $t$: $C = -6$

Coefficient of $t^2$: $A+B = 0 \implies 6+B=0 \implies B=-6$

Substitute these values back into the partial fraction form:

$\frac{6-6t}{t(1+t^2)} = \frac{6}{t} + \frac{-6t-6}{1+t^2} = \frac{6}{t} - \frac{6t}{1+t^2} - \frac{6}{1+t^2}$

Now, integrate each term:

$\int \left( \frac{6}{t} - \frac{6t}{1+t^2} - \frac{6}{1+t^2} \right) dt = 6 \int \frac{1}{t} dt - 6 \int \frac{t}{1+t^2} dt - 6 \int \frac{1}{1+t^2} dt$

$= 6 \ln|t| - 3 \ln(1+t^2) - 6 \arctan(t) + C'$

(For $\int \frac{t}{1+t^2} dt$, use substitution $u=1+t^2$, so $du=2t dt$, which gives $\int \frac{1}{2u} du = \frac{1}{2}\ln|u| = \frac{1}{2}\ln(1+t^2)$.)

Combine all parts of the integral:

$6t + 6 \ln|t| - 3 \ln(1+t^2) - 6 \arctan(t) + C$

Finally, substitute back $t = x^{1/6}$. Note that $t^2 = (x^{1/6})^2 = x^{2/6} = x^{1/3}$.

$6x^{1/6} + 6 \ln|x^{1/6}| - 3 \ln(1+x^{1/3}) - 6 \arctan(x^{1/6}) + C$

Using logarithm property $n \ln a = \ln a^n$:

$6x^{1/6} + \ln(x^{6 \times 1/6}) - 3 \ln(1+x^{1/3}) - 6 \arctan(x^{1/6}) + C$

$6x^{1/6} + \ln|x| - 3 \ln(1+x^{1/3}) - 6 \arctan(x^{1/6}) + C$

In radical notation:

$6\sqrt[6]{x} + \ln|x| - 3\ln(1+\sqrt[3]{x}) - 6\arctan(\sqrt[6]{x}) + C$

The final answer is $6\sqrt[6]{x} + \ln|x| - 3\ln(1+\sqrt[3]{x}) - 6\arctan(\sqrt[6]{x}) + C$.