Question

$\int \frac{sinx}{sinx+cosx}dx$

Answer 1

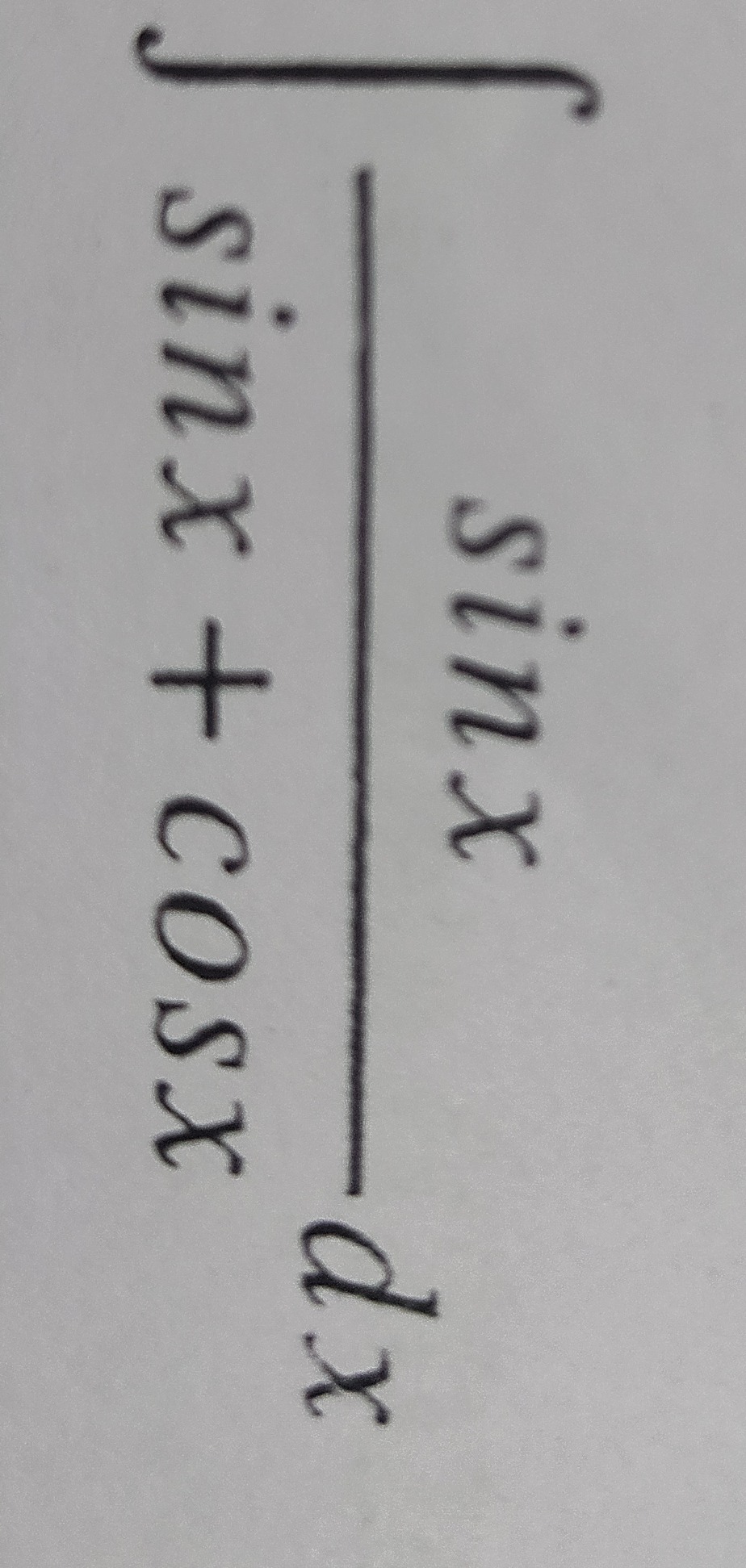
$\frac{1}{2}x - \frac{1}{2}\ln|\sin x + \cos x| + C$

Answer 2

To solve the integral $\int \frac{\sin x}{\sin x+\cos x}dx$, we use the technique of expressing the numerator as a linear combination of the denominator and its derivative.

Let the given integral be $I$. $I = \int \frac{\sin x}{\sin x+\cos x}dx$

Let $N(x) = \sin x$ (numerator) and $D(x) = \sin x + \cos x$ (denominator). The derivative of the denominator is $D'(x) = \cos x - \sin x$.

We aim to write the numerator $N(x)$ in the form $A \cdot D(x) + B \cdot D'(x)$, where $A$ and $B$ are constants. So, $\sin x = A(\sin x + \cos x) + B(\cos x - \sin x)$. Expand the right side: $\sin x = A\sin x + A\cos x + B\cos x - B\sin x$ Group terms by $\sin x$ and $\cos x$: $\sin x = (A-B)\sin x + (A+B)\cos x$

By comparing the coefficients of $\sin x$ and $\cos x$ on both sides:

1. Coefficient of $\sin x$: $1 = A-B$
2. Coefficient of $\cos x$: $0 = A+B$

From equation (2), we get $A = -B$. Substitute $A = -B$ into equation (1): $1 = (-B) - B$ $1 = -2B$ $B = -\frac{1}{2}$

Now find $A$: $A = -B = -(-\frac{1}{2}) = \frac{1}{2}$

So, we can write $\sin x$ as: $\sin x = \frac{1}{2}(\sin x + \cos x) - \frac{1}{2}(\cos x - \sin x)$

Substitute this expression back into the integral: $I = \int \frac{\frac{1}{2}(\sin x + \cos x) - \frac{1}{2}(\cos x - \sin x)}{\sin x+\cos x}dx$ Split the integral into two parts: $I = \int \left( \frac{\frac{1}{2}(\sin x + \cos x)}{\sin x+\cos x} - \frac{\frac{1}{2}(\cos x - \sin x)}{\sin x+\cos x} \right) dx$ $I = \int \left( \frac{1}{2} - \frac{1}{2} \frac{\cos x - \sin x}{\sin x+\cos x} \right) dx$

Now, integrate each term separately: $I = \frac{1}{2} \int dx - \frac{1}{2} \int \frac{\cos x - \sin x}{\sin x+\cos x} dx$

The first part is straightforward: $\frac{1}{2} \int dx = \frac{1}{2}x$

For the second part, let $u = \sin x + \cos x$. Then, differentiate $u$ with respect to $x$: $du = (\cos x - \sin x) dx$. So the second integral becomes: $\int \frac{du}{u} = \ln|u| + C_1 = \ln|\sin x + \cos x| + C_1$

Combining both parts, we get the final result: $I = \frac{1}{2}x - \frac{1}{2} \ln|\sin x + \cos x| + C$

The constant of integration $C$ is added at the end.

Explanation of the solution: The integral $\int \frac{\sin x}{\sin x+\cos x}dx$ is solved by expressing the numerator $\sin x$ as $A(\sin x+\cos x) + B(\cos x-\sin x)$. Comparing coefficients yields $A=1/2$ and $B=-1/2$. Substituting this back, the integral splits into $\int \frac{1}{2} dx - \int \frac{1}{2} \frac{\cos x-\sin x}{\sin x+\cos x} dx$. The first part integrates to $\frac{1}{2}x$. The second part is of the form $\int \frac{f'(x)}{f(x)} dx$, which integrates to $\ln|f(x)|$. Thus, the solution is $\frac{1}{2}x - \frac{1}{2}\ln|\sin x + \cos x| + C$.