Question
Question: $\int (\frac{sinx+sin2x+sin3x}{cosx+cos2x+cos3x})^2dx$...
∫(cosx+cos2x+cos3xsinx+sin2x+sin3x)2dx
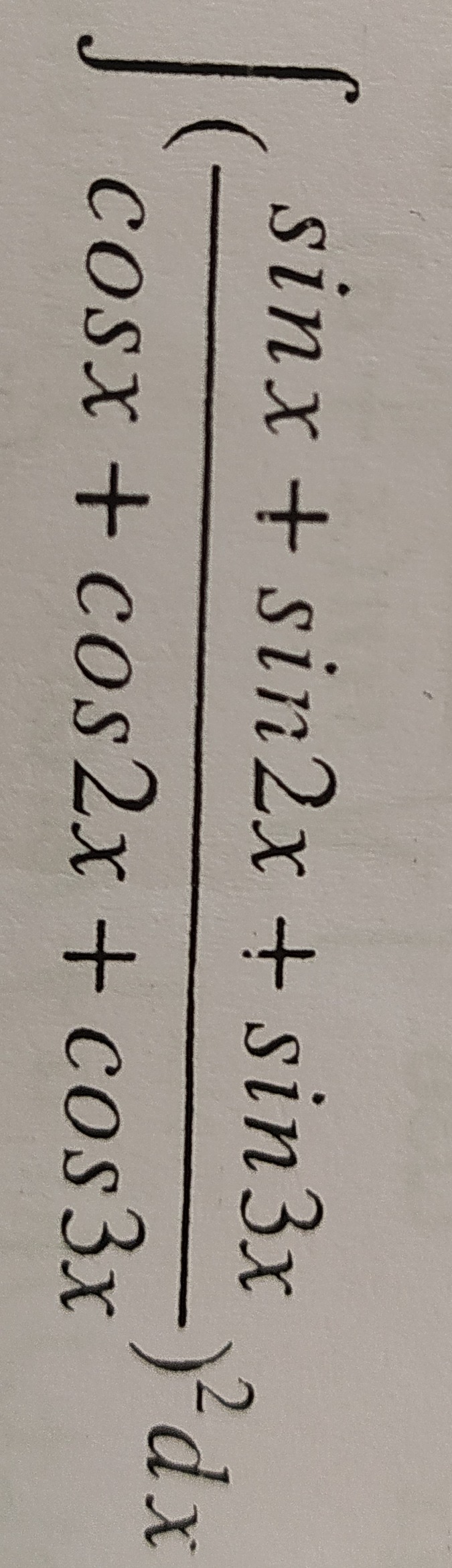
21tan(2x)−x+C
Solution
The problem asks to evaluate the integral ∫(cosx+cos2x+cos3xsinx+sin2x+sin3x)2dx.
Step 1: Simplify the trigonometric expression inside the integral. The expression is E=cosx+cos2x+cos3xsinx+sin2x+sin3x. We can rearrange the terms in the numerator and denominator and use the sum-to-product trigonometric identities: sinA+sinB=2sin(2A+B)cos(2A−B) cosA+cosB=2cos(2A+B)cos(2A−B)
Numerator: sinx+sin2x+sin3x=(sinx+sin3x)+sin2x =2sin(2x+3x)cos(2x−3x)+sin2x =2sin(2x)cos(−x)+sin2x =2sin(2x)cosx+sin2x (since cos(−x)=cosx) =sin2x(2cosx+1)
Denominator: cosx+cos2x+cos3x=(cosx+cos3x)+cos2x =2cos(2x+3x)cos(2x−3x)+cos2x =2cos(2x)cos(−x)+cos2x =2cos(2x)cosx+cos2x =cos2x(2cosx+1)
Now, substitute these back into the expression E: E=cos2x(2cosx+1)sin2x(2cosx+1) Assuming 2cosx+1=0, we can cancel the common term (2cosx+1): E=cos2xsin2x=tan2x
Step 2: Integrate the simplified expression. The integral becomes: I=∫(tan2x)2dx=∫tan2(2x)dx
We use the trigonometric identity tan2θ=sec2θ−1: I=∫(sec2(2x)−1)dx
Now, integrate term by term: I=∫sec2(2x)dx−∫1dx
For the first integral, ∫sec2(2x)dx, we use a substitution. Let u=2x, so du=2dx, which means dx=21du. ∫sec2(2x)dx=∫sec2(u)21du=21∫sec2(u)du We know that ∫sec2udu=tanu+C. So, 21tanu+C=21tan(2x)+C1.
For the second integral, ∫1dx=x+C2.
Combining the results: I=21tan(2x)−x+C where C=C1+C2 is the constant of integration.
The final answer is 21tan(2x)−x+C.
Explanation of the solution:
- Simplify the integrand: Use sum-to-product formulas for trigonometric functions to simplify the numerator and denominator. sinx+sin3x=2sin(2x)cosx cosx+cos3x=2cos(2x)cosx This leads to cos2x(2cosx+1)sin2x(2cosx+1)=tan2x.
- Rewrite the integral: The integral becomes ∫tan2(2x)dx.
- Apply trigonometric identity: Use tan2θ=sec2θ−1 to rewrite the integrand as sec2(2x)−1.
- Integrate: Integrate term by term. ∫sec2(2x)dx=21tan(2x) (using substitution u=2x). ∫1dx=x.
- Combine results: The final integral is 21tan(2x)−x+C.
Answer:
The integral is 21tan(2x)−x+C.
