Question

$\int \frac{sin\sqrt{x}}{\sqrt{x}} dx$

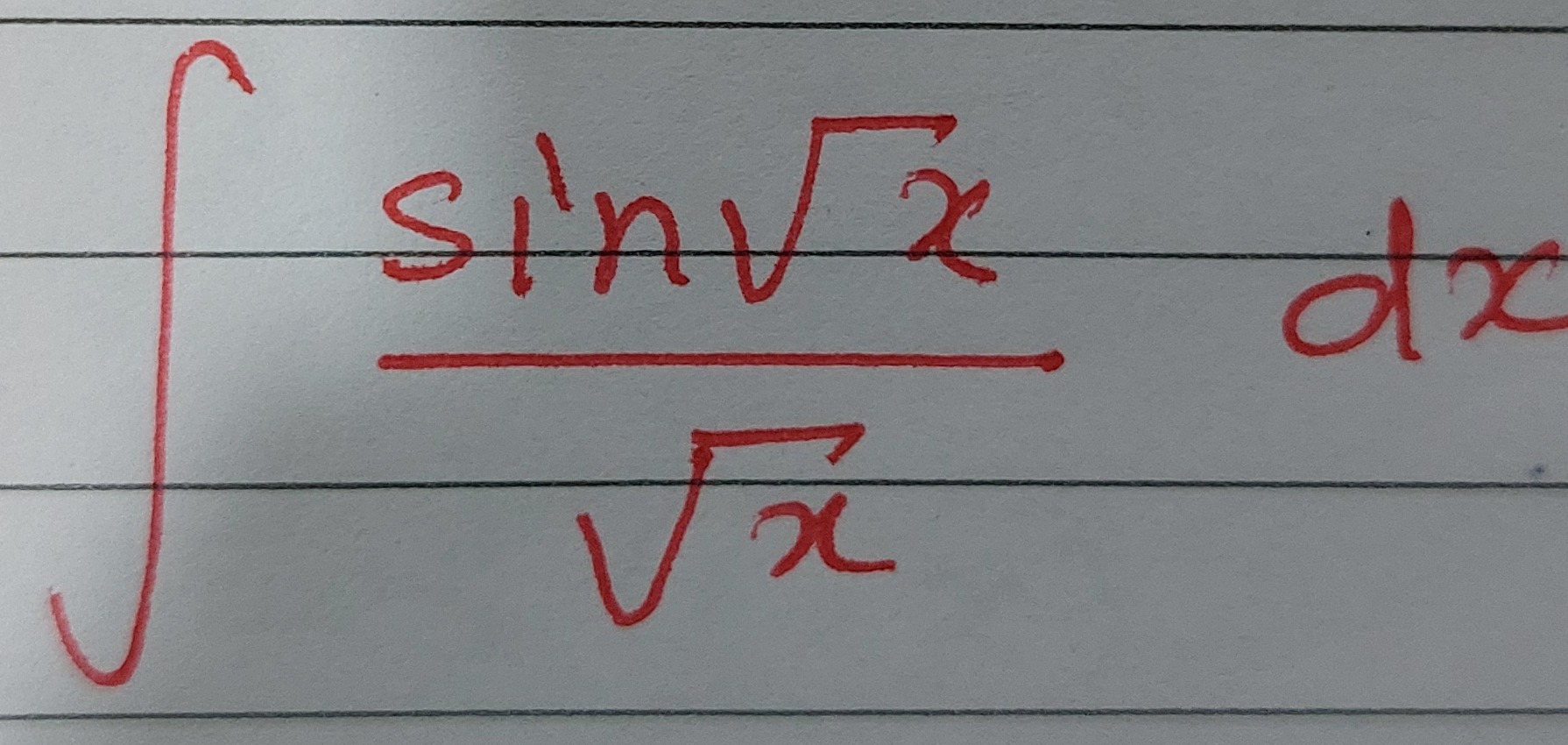
Answer 1

-2cos(√(x)) + C

Answer 2

Solution:

Let

$$u = \sqrt{x} \quad \Rightarrow \quad x = u^2 \quad \text{and} \quad dx = 2u\, du.$$

Substitute into the integral:

$$\int \frac{\sin \sqrt{x}}{\sqrt{x}}\,dx = \int \frac{\sin u}{u} \cdot (2u\,du) = 2\int \sin u\,du.$$

Now, integrate:

$$2\int \sin u\,du = 2(-\cos u) + C = -2\cos u + C.$$

Replacing back $u = \sqrt{x}$:

$$-2\cos(\sqrt{x}) + C.$$

Explanation:

Use substitution $u = \sqrt{x}$ to transform the integral into $2\int \sin u\,du$ which integrates to $-2\cos u + C$. Finally, revert back to $x$.