Question

$\int \frac{sin^6x + cos^6x}{sin^2x.cos^2x}dx$

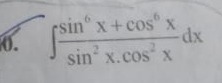
Answer 1

-2cot(2x) - 3x + C

Answer 2

Solution:

1. Rewrite the Numerator:

   $$\sin^6 x + \cos^6 x = (\sin^2 x + \cos^2 x)^3 - 3\sin^2 x \cos^2 x (\sin^2 x + \cos^2 x) = 1 - 3\sin^2 x\cos^2 x.$$

2. Simplify the Integrand:

   $$\frac{\sin^6 x + \cos^6 x}{\sin^2 x\cos^2 x} = \frac{1 - 3\sin^2 x \cos^2 x}{\sin^2 x\cos^2 x} = \frac{1}{\sin^2 x\cos^2 x} - 3.$$

3. Express in Terms of the Double Angle: Note that:

   $$\sin^2 x\cos^2 x = \frac{1}{4}\sin^2 (2x) \quad \Rightarrow \quad \frac{1}{\sin^2 x\cos^2 x} = \frac{4}{\sin^2 (2x)} = 4\,\csc^2 (2x).$$

4. Write the Integral Separately:

   $$\int \frac{\sin^6 x + \cos^6 x}{\sin^2 x\cos^2 x}\,dx = 4\int \csc^2(2x)\,dx - 3\int dx.$$

5. Integrate Each Part:

   • For $\int \csc^2(2x)\,dx$: Use substitution $u = 2x$ so that $du = 2dx$; hence, $$\int \csc^2(2x)\,dx = \frac{1}{2}\int \csc^2 u\,du = -\frac{1}{2}\cot u + C = -\frac{1}{2}\cot(2x) + C.$$
   • For $\int dx$: This is $x$.

6. Combine the Results:

   $$4\left(-\frac{1}{2}\cot(2x)\right) - 3x + C = -2\cot(2x) - 3x + C.$$

Explanation:

Use the sum-of-cubes identity to simplify the numerator, express in terms of double-angle, and integrate using the standard integral $\int \csc^2u\,du = -\cot u$.