Question

$\int \frac{sin^3x+cos^3x}{sin^2xcos^2x}dx$

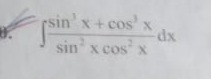
Answer 1

$\sec x - \csc x + C$

Answer 2

We start with

$$I = \int \frac{\sin^3 x + \cos^3 x}{\sin^2 x \cos^2 x}\,dx.$$

Step 1: Rewrite the integrand by splitting the fraction:

$$\frac{\sin^3 x}{\sin^2 x\cos^2 x} + \frac{\cos^3 x}{\sin^2 x\cos^2 x} = \frac{\sin x}{\cos^2 x} + \frac{\cos x}{\sin^2 x}.$$

Thus,

$$I = \int \frac{\sin x}{\cos^2 x}\,dx + \int \frac{\cos x}{\sin^2 x}\,dx.$$

Step 2: Evaluate the first integral. Let $u = \cos x$ so that $du = -\sin x\,dx$. Then:

$$\int \frac{\sin x}{\cos^2 x}\,dx = -\int \frac{du}{u^2} = \frac{1}{u} + C_1 = \sec x + C_1.$$

Step 3: Evaluate the second integral. Let $v = \sin x$ so that $dv = \cos x\,dx$. Then:

$$\int \frac{\cos x}{\sin^2 x}\,dx = \int \frac{dv}{v^2} = -\frac{1}{v} + C_2 = -\csc x + C_2.$$

Step 4: Combine the results.

$$I = \sec x - \csc x + C \quad \text{where } C = C_1 + C_2.$$