Question

\int \frac{sin(2-ex)}{cos^2(2-3x)}dx

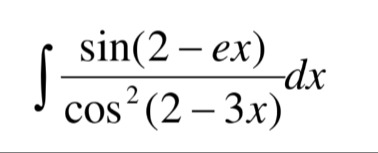
Answer 1

Assuming the question intended to be $\int \frac{\sin(2-3x)}{\cos^2(2-3x)}dx$, the answer is $-\frac{1}{3} \sec(2-3x) + C$.

Answer 2

Let $u = \cos(2-3x)$. Then $du = - \sin(2-3x) \cdot (-3) dx = 3 \sin(2-3x) dx$. So, $\sin(2-3x) dx = \frac{1}{3} du$. The integral becomes $\int \frac{1}{u^2} \cdot \frac{1}{3} du = \frac{1}{3} \int u^{-2} du = \frac{1}{3} \frac{u^{-1}}{-1} + C = -\frac{1}{3u} + C$. Substituting back $u = \cos(2-3x)$, we get $-\frac{1}{3\cos(2-3x)} + C = -\frac{1}{3} \sec(2-3x) + C$.