Question

$\int \frac{Sin \ x \cdot Cos \frac{5x}{2}}{Cos \frac{x}{2}} dx =$

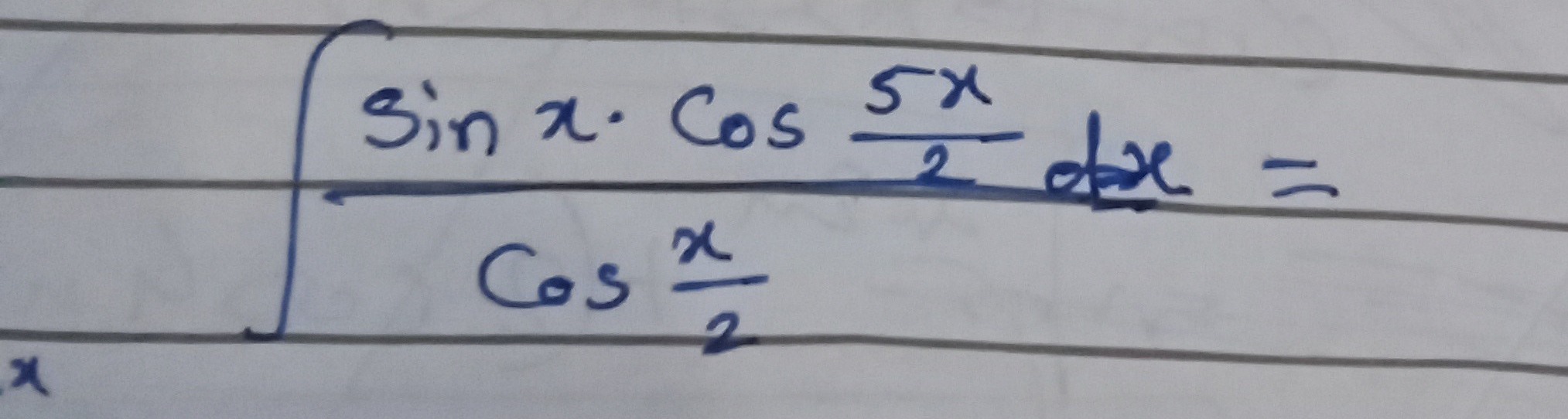
Answer 1

$\frac{1}{2}\cos 2x-\frac{1}{3}\cos3x+C.$

Answer 2

Solution:

Given the integral

$$I=\int \frac{\sin x\, \cos\frac{5x}{2}}{\cos\frac{x}{2}}\,dx,$$

Step 1: Use the identity $\sin x = 2\sin\frac{x}{2}\cos\frac{x}{2}$ to rewrite:

$$I=\int \frac{2\sin\frac{x}{2}\cos\frac{x}{2}\cdot\cos\frac{5x}{2}}{\cos\frac{x}{2}}\,dx =\int 2\sin\frac{x}{2}\cos\frac{5x}{2}\,dx.$$

Step 2: Apply the product-to-sum formula:

$$2\sin A\cos B = \sin(A+B)+\sin(A-B)$$

with $A=\frac{x}{2}$ and $B=\frac{5x}{2}$. Then,

$$2\sin\frac{x}{2}\cos\frac{5x}{2} = \sin\left(\frac{x}{2}+\frac{5x}{2}\right)+\sin\left(\frac{x}{2}-\frac{5x}{2}\right) =\sin3x+\sin(-2x)=\sin3x-\sin2x.$$

Step 3: Now the integral becomes:

$$I=\int \left(\sin3x-\sin2x\right)\,dx.$$

Integrate term-by-term:

$$\int \sin 3x\,dx = -\frac{1}{3}\cos3x,\quad \int \sin2x\,dx = -\frac{1}{2}\cos2x.$$

Thus,

$$I=-\frac{1}{3}\cos3x + \frac{1}{2}\cos2x + C.$$

---

Minimal Explanation:

1. Replace $\sin x$ by $2\sin\frac{x}{2}\cos\frac{x}{2}$ to cancel the denominator.

2. Use the product-to-sum formula to convert the product into sums of sines.

3. Integrate each sine term.

---

Mermaid Diagram: