Question
Question: $\int \frac{lnx-1}{(lnx)^2}dx$...
∫(lnx)2lnx−1dx
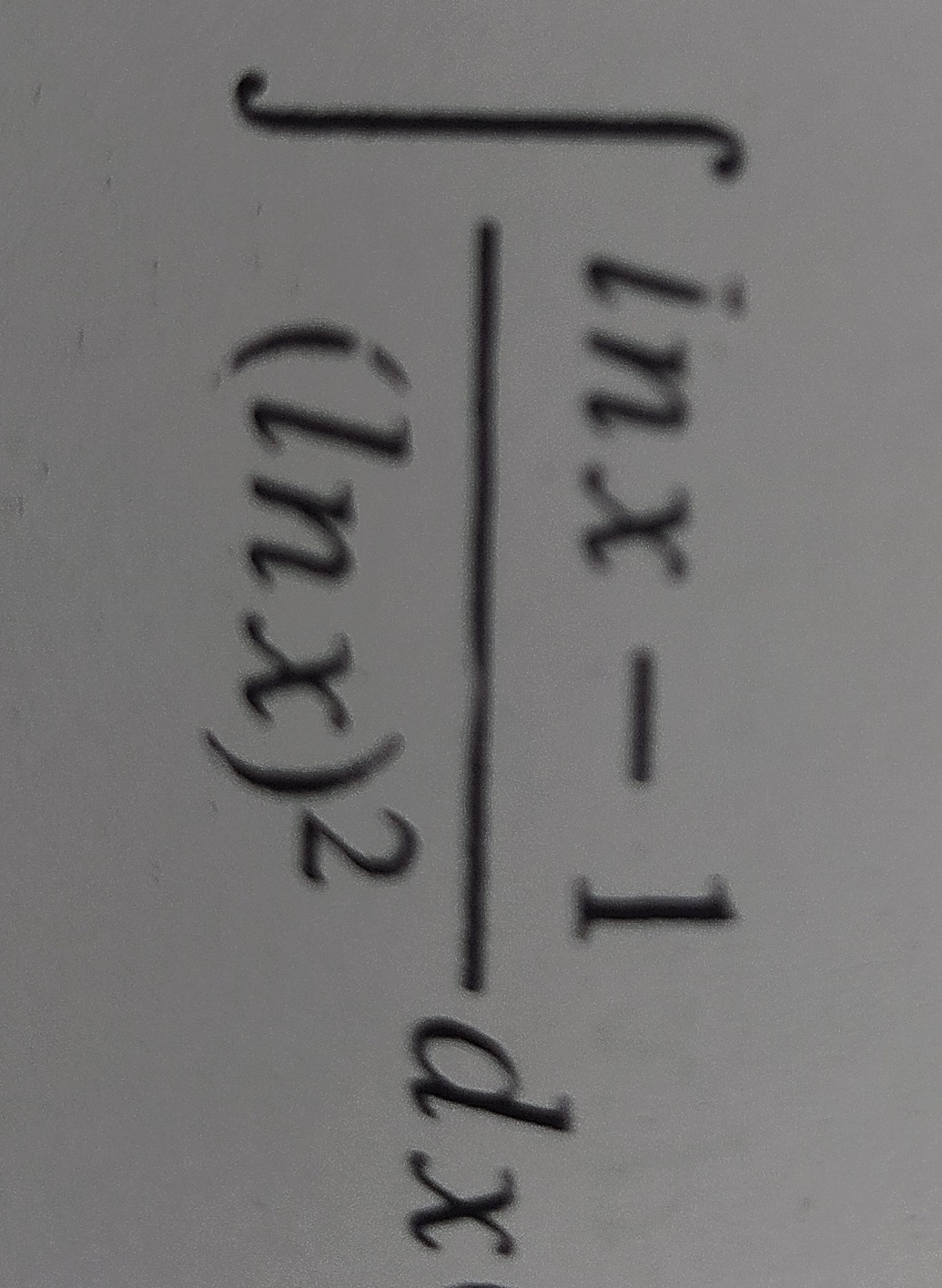
lnxx+C
Solution
To evaluate the integral ∫(lnx)2lnx−1dx, we can use a substitution method.
Let t=lnx.
From this substitution, we can express x in terms of t:
x=et.
Now, differentiate x=et with respect to t to find dx:
dx=etdt.
Substitute t and dx into the integral: ∫(lnx)2lnx−1dx=∫t2t−1etdt
Rearrange the terms inside the integral: ∫(t2t−t21)etdt=∫(t1−t21)etdt
This integral is of the form ∫ex(f(x)+f′(x))dx=exf(x)+C.
In our case, let f(t)=t1.
Then, the derivative of f(t) with respect to t is f′(t)=−t21.
So, the integral matches the form ∫et(f(t)+f′(t))dt.
Applying the formula, the integral evaluates to:
etf(t)+C=et⋅t1+C
Finally, substitute back t=lnx into the result: elnx⋅lnx1+C Since elnx=x, the expression simplifies to: x⋅lnx1+C=lnxx+C
To verify the result, differentiate lnxx with respect to x using the quotient rule:
Let u=x and v=lnx. Then u′=1 and v′=x1.
dxd(lnxx)=v2u′v−uv′=(lnx)21⋅lnx−x⋅x1=(lnx)2lnx−1
This matches the original integrand, confirming the correctness of the solution.
