Question

\int \frac{e^{4x}}{1+e^{-x}} =

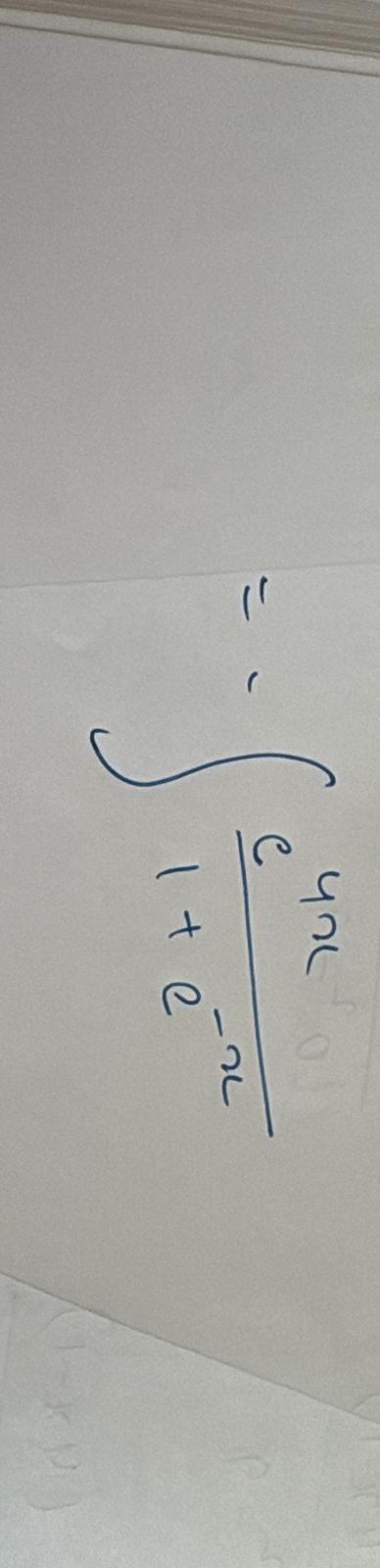
Answer 1

\frac{e^{4x}}{4} - \frac{e^{3x}}{3} + \frac{e^{2x}}{2} - e^x + \ln(e^x+1) + C

Answer 2

Simplify the integrand to $\frac{e^{5x}}{e^x+1}$. Substitute $u=e^x$, transforming the integral to $\int \frac{u^4}{u+1} du$. Decompose $\frac{u^4}{u+1}$ into $u^3 - u^2 + u - 1 + \frac{1}{u+1}$. Integrate term-by-term and substitute back $u=e^x$ to obtain the final result.