Question

$\int \frac{dx}{x^2-a^2} dx = \frac{1}{2a} ln \left| \frac{x-a}{x+a} \right| + C$

Answer 1

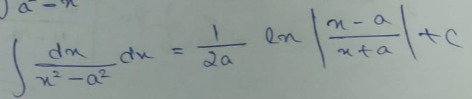
The given formula is correct.

Answer 2

To evaluate the integral $\int \frac{dx}{x^2-a^2}$, we use the method of partial fraction decomposition.

Step 1: Factor the denominator

The denominator $x^2-a^2$ is a difference of squares, which can be factored as $(x-a)(x+a)$.
So the integral becomes:

$\int \frac{dx}{(x-a)(x+a)}$

Step 2: Decompose the integrand into partial fractions

We assume that $\frac{1}{(x-a)(x+a)}$ can be written as the sum of two simpler fractions:

$\frac{1}{(x-a)(x+a)} = \frac{A}{x-a} + \frac{B}{x+a}$

To find the constants $A$ and $B$, we multiply both sides by $(x-a)(x+a)$:

$1 = A(x+a) + B(x-a)$

Now, we can find $A$ and $B$ by substituting specific values for $x$:

• Set $x=a$:

  $1 = A(a+a) + B(a-a)$

  $1 = A(2a) + B(0)$

  $1 = 2aA \implies A = \frac{1}{2a}$

• Set $x=-a$:

  $1 = A(-a+a) + B(-a-a)$

  $1 = A(0) + B(-2a)$

  $1 = -2aB \implies B = -\frac{1}{2a}$

Step 3: Substitute the partial fractions back into the integral

Now, the integral can be written as:

$\int \left( \frac{1}{2a(x-a)} - \frac{1}{2a(x+a)} \right) dx$

We can factor out $\frac{1}{2a}$:

$\frac{1}{2a} \int \left( \frac{1}{x-a} - \frac{1}{x+a} \right) dx$

Step 4: Integrate term by term

We know that $\int \frac{1}{u} du = \ln|u| + C$.

$\frac{1}{2a} \left( \int \frac{1}{x-a} dx - \int \frac{1}{x+a} dx \right)$

$= \frac{1}{2a} \left( \ln|x-a| - \ln|x+a| \right) + C$

Step 5: Apply logarithm properties

Using the logarithm property $\ln P - \ln Q = \ln \left(\frac{P}{Q}\right)$:

$= \frac{1}{2a} \ln \left| \frac{x-a}{x+a} \right| + C$

This result matches the formula provided in the question.

The given formula is correct.