Question
Question: $\int \frac{dx}{(x+1)\sqrt{x^2+4}} =$...
∫(x+1)x2+4dx=
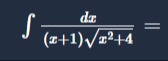
A
51lnx+1x2+4−x+2+C
B
51lnx+1x2+4−x−2+C
C
51lnx+1x2+4+x−2+C
D
51lnx+1x2+4−x+4+C
Answer
51lnx+1x2+4+x−2+C
Explanation
Solution
Let the given integral be I=∫(x+1)x2+4dx. We use the substitution x+1=t1. Then x=t1−1, and dx=−t21dt. Also, x2+4=(t1−1)2+4=t2(1−t)2+4=t21−2t+t2+4t2=t25t2−2t+1. So, x2+4=t25t2−2t+1=∣t∣5t2−2t+1.
The integral becomes I=∫t1⋅∣t∣5t2−2t+1−t21dt.
