Question
Question: $\int \frac{dx}{\sqrt{x^2+1}+\sqrt{x^2-1}}$...
∫x2+1+x2−1dx
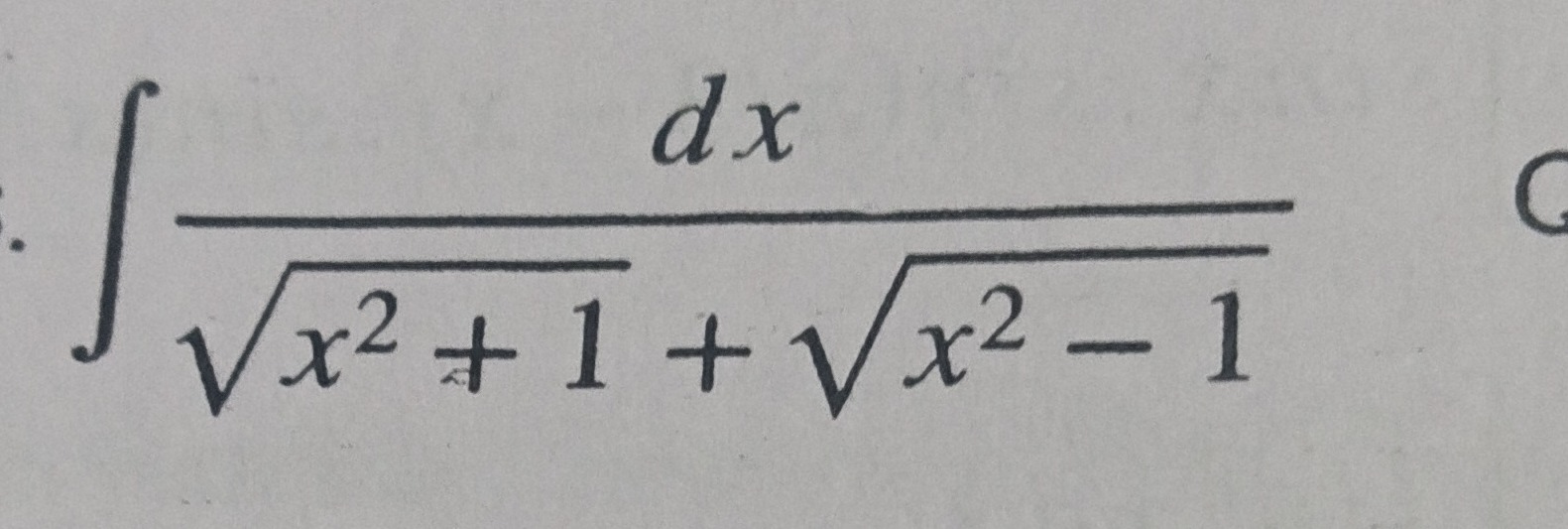
4x(x2+1−x2−1)+41(ln∣x+x2+1∣+ln∣x+x2−1∣)+C
Solution
To evaluate the integral ∫x2+1+x2−1dx, we first rationalize the denominator.
Step 1: Rationalize the Denominator
Multiply the numerator and the denominator by the conjugate of the denominator, which is x2+1−x2−1.
x2+1+x2−11=x2+1+x2−11×x2+1−x2−1x2+1−x2−1Using the identity (a+b)(a−b)=a2−b2 in the denominator:
=(x2+1)2−(x2−1)2x2+1−x2−1 =(x2+1)−(x2−1)x2+1−x2−1 =x2+1−x2+1x2+1−x2−1 =2x2+1−x2−1Step 2: Integrate the Simplified Expression
Now, substitute this simplified expression back into the integral:
∫x2+1+x2−1dx=∫2x2+1−x2−1dx =21[∫x2+1dx−∫x2−1dx]Step 3: Apply Standard Integration Formulas
We use the standard integration formulas:
- ∫x2+a2dx=2xx2+a2+2a2ln∣x+x2+a2∣+C
- ∫x2−a2dx=2xx2−a2−2a2ln∣x+x2−a2∣+C
For the first integral, ∫x2+1dx, we have a=1:
∫x2+1dx=2xx2+1+212ln∣x+x2+1∣=2xx2+1+21ln∣x+x2+1∣For the second integral, ∫x2−1dx, we have a=1:
∫x2−1dx=2xx2−1−212ln∣x+x2−1∣=2xx2−1−21ln∣x+x2−1∣Step 4: Combine the Results
Substitute these back into the expression from Step 2:
21[(2xx2+1+21ln∣x+x2+1∣)−(2xx2−1−21ln∣x+x2−1∣)]+C =21[2xx2+1+21ln∣x+x2+1∣−2xx2−1+21ln∣x+x2−1∣]+CDistribute the 21:
=4xx2+1−4xx2−1+41ln∣x+x2+1∣+41ln∣x+x2−1∣+CThis can also be written by factoring out common terms:
=4x(x2+1−x2−1)+41(ln∣x+x2+1∣+ln∣x+x2−1∣)+CThe final answer is 4x(x2+1−x2−1)+41(ln∣x+x2+1∣+ln∣x+x2−1∣)+C.
Explanation of the solution: The integral is simplified by rationalizing the denominator, which transforms the integrand into a difference of two standard forms (x2+a2 and x2−a2). Each part is then integrated using their respective standard formulas, and the results are combined.
