Question
Question: $\int \frac{dx}{\sin^2x \cos^2x}$ is equal to...
∫sin2xcos2xdx is equal to
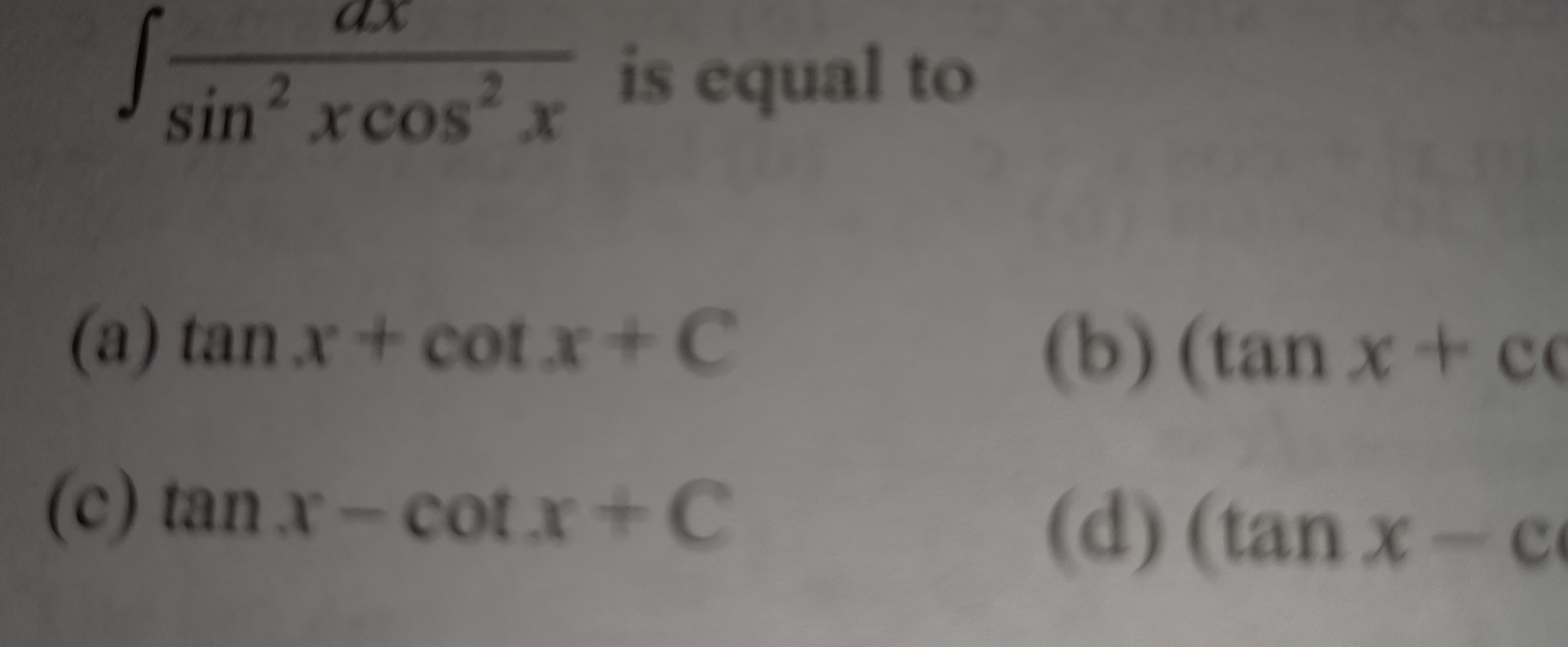
tan x + cot x + C
(tan x + co
tan x - cotx + C
(tan x - c
tan x - cot x + C
Solution
To evaluate the integral ∫sin2xcos2xdx, we can use trigonometric identities.
We know that sin2x+cos2x=1. We can substitute this into the numerator of the integrand: ∫sin2xcos2x1dx=∫sin2xcos2xsin2x+cos2xdx
Now, we can split the fraction into two terms: ∫(sin2xcos2xsin2x+sin2xcos2xcos2x)dx
Simplify each term: ∫(cos2x1+sin2x1)dx
Recall the reciprocal trigonometric identities: cosx1=secx and sinx1=cscx. So, cos2x1=sec2x and sin2x1=csc2x. ∫(sec2x+csc2x)dx
Now, integrate each term separately using the standard integration formulas: ∫sec2xdx=tanx+C1 ∫csc2xdx=−cotx+C2
Combining these results, the integral is: tanx−cotx+C where C=C1+C2 is the constant of integration.
